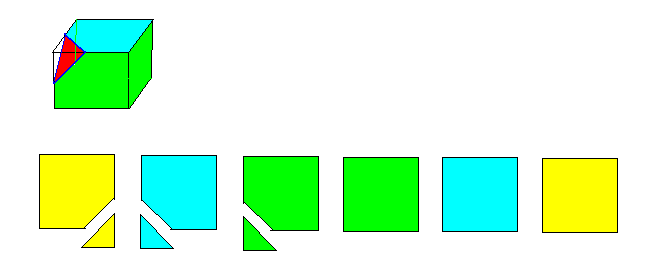
 図のような立方体を1つの平面で切る。展開図にしたとき正方形がいくつかの部分
に分かれる。いくつに分かれる可能性があるか。なお、のりしろ部分は考えないも
のとする。
図のような立方体を1つの平面で切る。展開図にしたとき正方形がいくつかの部分
に分かれる。いくつに分かれる可能性があるか。なお、のりしろ部分は考えないも
のとする。
【傾向】 97年度の問10は、袋の中の玉を移す確率の問題である。組合せの計算を 使って解くと良い。問12は四則演算の問題をツリー構造で表現した問題で ある。形に惑わされなければよい。問19は空間図形の展開図の問題だが、 立体視の能力を問うている。
1997年度問題
問10 Aの袋には白玉が4つ黒玉が3つ、Bの袋には白玉が3つ黒玉が2つ入っている。 Aの袋から玉を3つ取り出してBの袋に入れ、その後Bの袋から玉を2つ取り出し てAの袋に入れる。このときAの袋が白玉だけになる確率を求めよ。 問12 四則計算を次の形で示す。 (例) (×) (+) / \ / \ / \ (A) (B) (+) (-) / \ / \ A+B (A) (B) (C) (D) (A+B)×(C-D) 以上の四則演算に従い、下記の2つの演算結果の合計を求めよ。 (+) / \ / \ (-) (+) / \ / \ (×) (÷) (×) (-) / \ / \ / \ / \ 251 (-)105 5 50 40 140 20 / \ 120 109 (-) / \ / \ (×) (+) / \ / \ (+) (-) 341 (×) / \ / \ / \ -30 32 321 101 251 (÷) / \ 72 8 問19図のような立方体を1つの平面で切る。展開図にしたとき正方形がいくつかの部分 に分かれる。いくつに分かれる可能性があるか。なお、のりしろ部分は考えないも のとする。
1997年度解答
from=武田
問103 C3 3 C2 3・2・1 3・2 1 3 3 ───×───=─────×───=──×──=─── ……(答) 7 C3 8 C2 7・6・5 8・7 35 28 980 問12 上の演算の左側は 251×(120-109)-(105÷5)=251×11-21=2740 右側は 50×40+(140-20)=2000+120=2120 最後に 2740+2120=4860……① 下の演算の左側は (-30+32)×(321-101)=2×220=440 右側は 341+{251×(72÷8)}=341+251×9=341+2259=2600 最後に 440-2600=-2160……② 2つの演算結果の合計は①と②より、 4860+(-2160)=2700 ……(答) 問19
図のように切ると、①は9個に分かれる。②は10個に分かれる。③は12個に分かれる。 ④は11個に分かれる。⑤は8個に分かれる。 したがって、 答は、8,9,10,11,12に分かれる可能性がある。