教員試験一般教養（数学）１９９８

【傾向】
９８年度の問９は、図形の辺に向きと大きさを与えているので、立体視の能
力とベクトルの考えを使って作られている。問１０は階段の登り方の問題だ
が、階段を１段ずつ増やしていくとフィボナッチ数列の問題となる。８段の
みで考えると、場合の数の組合せを使って解くことになる。問１１はクイズ
の穴埋め問題だが、数の配置を考えながら解くわけだが、必ずどこかに解く
キッカケがある。この問題では百の位のＢである。問１２は四則演算の問題
を少し変形したものである。◎などの記号演算に慣れてないと惑うところが
ある。

１９９８年度問題

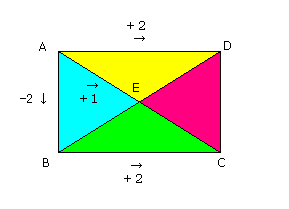
問９
　　　　　　　　　　　　　　　　+2　　　　　　　　　　　　　　　　□
Ａ地点からＢ地点が２高いとき、Ａ→Ｂと示すこととする。次の場合、Ｃ→Ｄとなる。
□に入る数はいくつになるか。


問１０
８段ある階段を「１段ずつ登る」「２段ずつ登る」「１段と２段を混ぜて登る」ことに
した。階段の登り方は全部で何通りあるか。

問１１
下の計算において、Ａ～Ｄには１から９までの異なる自然数が当てはまる。このとき、
Ａ×Ｂ×Ｃ×Ｄの値はいくつになるか。

　　　　　　　　　ＡＢＤＢ
　　　　　　　　＋ＡＢＣＤ
　　　　　　　　──────
　　　　　　　　　ＢＢＡＣ

問１２
｛（６△３）☆５｝◎６＝２８▽２と成り立っている式がある。それぞれの記号の意味
は、ａ◎ｂ＝３ａｂ、ａ△ｂ＝２ａ＋ｂ、ａ▽ｂ＝２ａ－ｂである。このとき、ａ☆ｂ
が表す式として正しいものを選びなさい。
（１）ａ÷ｂ　（２）ａ2 ｂ　（３）３ａ－ｂ
（４）（ａ＋ｂ）（ａ－ｂ）　（５）ａ2 ＋ｂ2 

１９９８年度解答
from=武田

問９
　-2　　　+1　　　　　+3
Ａ→Ｂ、Ａ→Ｅより、Ｂ→Ｅ
　+3　　　+2　　　　　-1
Ｂ→Ｅ、Ｂ→Ｃより、Ｅ→Ｃ
　+2　　　+1　　　　　+1
Ａ→Ｄ、Ａ→Ｅより、Ｅ→Ｄ
　+1　　　-1　　　　　+2
Ｅ→Ｄ、Ｅ→Ｃより、Ｃ→Ｄ
したがって、□＝+2……（答）

問１０

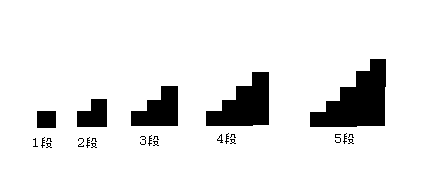階段が１段のとき、１通り
階段が２段のとき、２通り
階段が３段のとき、３通り
階段が４段のとき、５通り
階段が５段のとき、８通り
この数列はフィボナッチ数列にとなるので、
６段のとき、５＋８＝１３通り
７段のとき、８＋１３＝２１通り
８段のとき、１３＋２１＝３４通り
したがって、３４通り……（答）

問１１

　　　　　　　　　ＡＢＤＢ
　　　　　　　　＋ＡＢＣＤ
　　　　　　　　──────
　　　　　　　　　ＢＢＡＣ

百の位より、Ｂ＋Ｂ＝Ｂとなるのは繰り上がりがあるときのＢ＝９である。
千の位より、Ａ＋Ａ＝９。百の位から１繰り上がるから、Ａ＋Ａ＝８
したがって、Ａ＝４
９＋Ｄ＝１０＋Ｃ
Ｄ＋Ｃ＝１０＋（４－１）
上の連立を解いて、９－Ｃ＝Ｃ－３
　　　　　　　　　２Ｃ＝１２
　　　　　　　　　∴Ｃ＝６
したがって、Ｄ＝（１０－９）＋Ｃ
　　　　　　　＝１＋６＝７
Ａ×Ｂ×Ｃ×Ｄ＝４×９×６×７＝１５１２……（答）

問１２
｛（６△３）☆５｝◎６＝２８▽２より、
６△３＝２・６＋３＝１５
１５☆５＝Ｘとおくと、
Ｘ◎６＝３・Ｘ・６＝１８Ｘ
２８▽２＝２・２８－２＝５４より、
１８Ｘ＝５４
したがって、Ｘ＝３
１５☆５＝３
∴ａ☆ｂ＝ａ÷ｂ……（答）