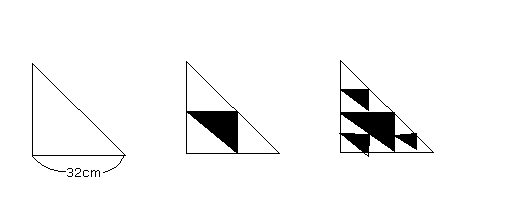問１８
正の数Ｘにおいて、［Ｘ］がＸの整数部分を示し、（Ｘ）はＸの小数部分
を示すとするとき、次の式を解きなさい。
（例）［７．２］＝７、（７．２）＝０．２
［７．６×３．４］ ［７．６×３．４］
［─────────－（８÷５）］－（─────────－（８÷５））
８ ８
【傾向】 ９９年度の問１６は、比の問題である。問１７は、面積の問題で、変化し ていく様子を調べれば答は求められる。問１８はガウスの記号もどきの演算 法則を決めて解く問題である。四則演算に自由さを体得しておけば解けるだ ろう。この年は、それ以前に比べて、比較的基礎問題がでたようだ。一般教 養の数学であれば、こういう問題の方が妥当であろう。
１９９９年度問題
問１６ 兄弟３人で車を購入するとき、長男Ａ，次男Ｂ，三男Ｃの出資率は、 Ａ：Ｂ＝５：３ Ｂ：Ｃ＝５：２ である。長男が１５０万円出資したとき、この車の購入金額はいくらか。 問１７ 図のような直角二等辺三角形の内部に図のような逆向きの黒い直角三角形 をかいていくものとする。３回目にかいたときの白い部分の面積を求めよ。
１９９９年度解答
from=武田
問１６ Ａ：Ｂ：Ｃ＝５×５：３×５：３×２ ＝２５：１５：６ ＝１５０万：９０万：３６万 したがって、 １５０万＋９０万＋３６万＝２７６万（円）……（答） 問１７ ３２×３２÷２＝５１２（ｃｍ2 ） 次の三角形の白い部分の面積は ３ ５１２×─＝３８４（ｃｍ2 ） ４ ２番目の三角形の白い部分の面積は ９ ５１２×──＝２８８（ｃｍ2 ） １６ ９ ３ ──＝（ ─ ）2 より、 １６ ４ 問題の３番目の白い部分の面積は ３ ５１２×（ ─ ）3 ＝２１６（ｃｍ2 ）……（答） ４ 問１８ ［７．６×３．４］ ［７．６×３．４］ ［─────────－（８÷５）］－（─────────－（８÷５）） ８ ８ ２５ ２５ ＝［ ── －０．６ ］－（ ── －０．６ ） ８ ８ ＝［ ３．１２５－０．６ ］－（ ３．１２５－０．６ ） ＝［ ２．５２５ ］－（ ２．５２５ ） ＝２－０．５２５ ＝１．４７５……（答）