問1 ΔABCにおいて、a=x+2,b=x+3,c=x+4とする。
(1)a,b,c,が三角形3辺の長さとなるためのxの値の範囲を求めよ。
(2)a,b,c,が鈍角三角形となるためのxの値の範囲を求めよ。
問2 一直線に並ぶ水平面上の3点A,B,Cから山頂 P の迎角を測ると、
それぞれ30°、60°、45°であった。
AB=200m、BC=100mであるとき山の高さを求めよ。
問3 ΔABCにおいて、次の等式が成り立つとき、この三角形は、それ
ぞれどのような三角形か。
(1)asinA+bsinB=csinC
(2)b=2acosC
(3)bcosA+acosB=b
問1
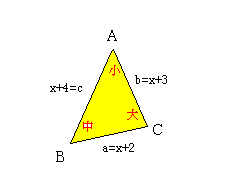
(1)a+b>cより、
(x+2)+(x+3)>x+4
2x+5>x+4
∴x>-1……(答)
(2)∠Cが最大なので、ここが鈍角となる。
余弦定理を利用して、
a2+b2-c2
cosC=────────
2ab
90°<∠C<180°より、
-1<cosC<0
a2+b2-c2
-1<────────<0
2ab
-2ab<a2+b2-c2<0
したがって、
{-2ab<a2+b2-c2……①
{a2+b2-c2<0……②
①より、c2<(a+b)2
c>0より、c<a+b∴x>-1……③
②より、a2+b2<c2
(x+2)2+(x+3)2<(x+4)2
x2+2x-3<0
(x+3)(x-1)<0
∴-3<x<1……④
③④より、
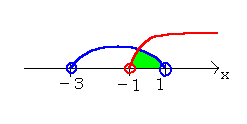
∴-1<x<1……(答)
問2
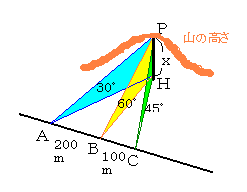
山の高さPH=xとおくと、
△PAHより、PA=2x
2x
△PBHより、PB=───
\(\sqrt{\quad}\)3
△PCHより、PC=\(\sqrt{\quad}\)2x
スチュワート(1717-1785)の定理
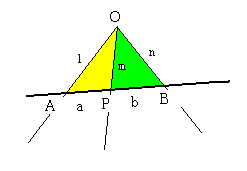
bl2+an2
───────=m2+ab
a+b
にあてはめると、
100・4x2+200・2x2 4x2
───────────────=───+200・100
200+100 3
800x2 4x2
─────=───+20000
300 3
800x2=400x2+6000000
400x2=6000000
x2=15000
∴x=50\(\sqrt{\quad}\)6≒122m……(答)
問3
(1)asinA+bsinB=csinC
正弦定理
a b c
───=───=───=2Rより、
sinA sinB sinC
a b c
sinA=───、sinB=──、sinC=───を与式に代入して、
2R 2R 2R
a2 b2 c2
───+───=───
2R 2R 2R
a2+b2=c2
∴∠Cが直角となる直角三角形……(答)
(2)b=2acosC
第2余弦定理その2
a2+b2-c2
cosC=──────── より、
2ab
a2+b2-c2
b=──────────
b
b2=a2+b2-c2
a2-c2=0
a2=c2
∴a=cとなる二等辺三角形……(答)
(3)bcosA+acosB=b
第1余弦定理
bcosA+acosB=c より、
c=b
∴b=cとなる二等辺三角形……(答)