武田先生おはようございます。
微分のところを勉強していてわからないところが
2題ほどあるので教えていただけないでしょうか?
問1
aを実数とする。曲線y=\(e^{x}\)上の各点における法線のうちで
点P(a.3)を通るものの個数をn(a)とする
n(a)を求めよ
問2
xの方程式 alog(x+a)+(\(\frac{a}{2}\))\(x^{2}\)-x=0はただ一つの
実数解をもつことを示せ。
ただしaは正の実数とし対数は自然対数とする。
問1
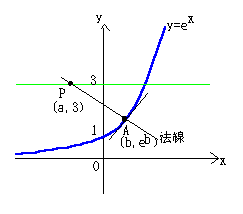
曲線上の点A(b,eb )から法線の方程式を求めると、
1
y-eb =-──(x-b)
eb
この直線が点P(a,3)を通るから
1
3-eb =-──(a-b)
eb
3eb -e2b=-a+b
a=b+e2b-3eb
左辺と右辺を別々にしてグラフを書く。そこで右辺の変数bを変数x
に変えると、
{y=a……①
{y=x+e2x-3ex ……②
②のグラフを書くために、微分して、
y′=1+2e2x-3ex
y′=0より、
2e2x-3ex+1=0
(2ex-1)(ex-1)=0
ex=1/2,ex=1
x=log(1/2),x=log1
∴x=-log2,x=0
増減表
x |…… |-log2|…… | 0 |……
────────────────────────
y′| + | 0 | - | 0 | +
────────────────────────
y | 増加| | 減少| | 増加
f′(-2log2)=1+2・2-4-3・2-2
=1+1/8-3/4=3/8>0
f′(-log1.5)=1+2・4/9-3・2/3
=1+8/9-2=-1/9<0
f′(log2)=1+2・4-3・2
=1+8-6=3>0
極大値f(-log2)=-log2+1/4-3/2=-5/4-log2
極小値f(0)=0+1-3=-2

このグラフと直線y=aとの交点から、個数n(a)を考えて、
(答){n(a<-2)=1
{n(-2)=n(-5/4-log2)=2
{n(-2<a<-5/4-log2)=3
{n(a>-5/4-log2)=1
問2
a
alog(x+a)+──x2 -x=0
2
左辺をf(x)とおいて、
a
f(x)=alog(x+a)+──x2 -x
2
微分して、
a a+ax2 -x+a2 x-a
f′(x)=───+ax-1=─────────────
x+a x+a
ax2 +(a2 -1)x x(ax+a2 -1)
=───────────=──────────
x+a x+a
f′(x)=0より、
1-a2
∴x=0,x=────,x≠-a
a
f(0)=aloga
1-a2 1-a2 a 1-a2 1-a2
f(────)=alog(─────+a)+──(─────)2 -─────
a a 2 a a
a4 -1
=-aloga+─────
2a
1-a2
①0<────の場合
a
(1-a)(1+a)>0
(a-1)(a+1)<0
∴-1<a<1
条件よりa>0
したがって、0<a<1
増減表
x |-a |…… | 0 |…… |(1-a2 )/a|……
───────────────────────────────────
f′(x)| / | + | 0 | - | 0 | +
───────────────────────────────────
f(x) | / | 増加| | 減少| | 増加
0<a<1より、
f(0)=aloga<0
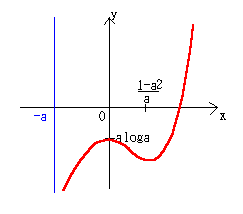
図より、x軸との交点が1つだから、f(x)=0の実数解は1個
1-a2
②0=────の場合
a
(1-a)(1+a)=0
∴a=1,a=-1
条件よりa>0
したがって、a=1
増減表
x |-1 |…… | 0 |……
─────────────────────
f′(x)| / | + | 0 | +
─────────────────────
f(x) | / | 増加| | 増加
a=1より、
f(0)=aloga=log1=0
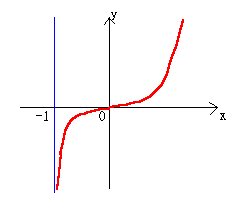
図より、x軸との交点が1つだから、f(x)=0の実数解は1個
1-a2
③0>────の場合
a
(1-a)(1+a)<0
(a-1)(a+1)>0
∴a<-1,1<a
条件よりa>0
したがって、1<a
増減表
x |-a |…… |(1-a2 )/a|…… | 0 |……
───────────────────────────────────
f′(x)| / | + | 0 | - | 0 | +
───────────────────────────────────
f(x) | / | 増加| | 減少| | 増加
1<aより、
f(0)=aloga>0
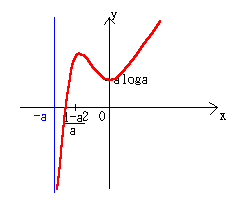
図より、x軸との交点が1つだから、f(x)=0の実数解は1個
したがって、①②③より、
a>0のとき、f(x)=0は、ただ1個の実数解をもつ。