昨日出された日々課題で分からない所がありましたので
質問させていただきます。宜しくお願いします。
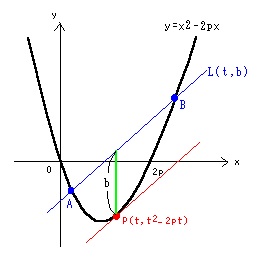
放物線y=x2 -2px上の点(t,t2 -2pt)
における接線をy軸方向にbだけ平行移動した直線を
L(t,b)とする。
(1)直線L(t,b)の方程式を求めよ。
(2)この放物線と直線L(t,b)とが、異なる2点で交わるための
t,bの範囲を求めよ。
(3)放物線と直線L(t,b)とが異なる2点で交わるとき、 これらが囲む図形の面積Sを求めよ。
(4)(3)の図形の面積を直線x=uで2等分したい。
uを求めよ。
問1
微分して、f′(x)=2x-2p
点P(t,t2 -2pt)における接線の方程式は
y-(t2 -2pt)=(2t-2p)(x-t)
この接線をy軸方向にbだけ平行移動すると、直線L(t,b)ができます。
この方程式は
y=(2t-2p)(x-t)+(t2 -2pt)+b……(答)
問2
上の直線L(t、b)と放物線y=x2 -2pxとの交点が2つあるのは、
連立して
{y=(2t-2p)(x-t)+(t2 -2pt)+b……①
{y=x2 -2px……②
(2t-2p)(x-t)+(t2 -2pt)+b=x2 -2px
x2 -2tx+t2 -b=0
判別式D/4>0より、
(-t)2 -(t2 -b)>0∴b>0……(答)
問3方程式x2 -2tx+t2 -b=0を解く。
∴x=t\(\pm\)\(\sqrt{\quad}\)b
したがって、
t+\(\sqrt{\quad}\)b
S=∫ {-(x2 -2tx+t2 -b)}dx
t-\(\sqrt{\quad}\)b
x3 t+\(\sqrt{\quad}\)b
=[-─ +tx2 -(t2 -b)x]
3 t-\(\sqrt{\quad}\)b
4
=(略)=─b\(\sqrt{\quad}\)b ……(答)
3
問4
4 t+\(\sqrt{\quad}\)b
─b\(\sqrt{\quad}\)b=2・∫ {-(x2 -2tx+t2 -b)}dx
3 u
(途中略)
u3 -3tu2 -3(t2 -b)u+(5t3 +6\(\sqrt{\quad}\)bt2 -3bt-6b\(\sqrt{\quad}\)b)=0
このuについての3次方程式は解けるのかな?
u=λ+tとおくと、
(途中略)
λ3 -(6t2 -3b)λ+(6t2 \(\sqrt{\quad}\)b-6b\(\sqrt{\quad}\)b)=0
さて、これ以上は解けない。λが出れば、uも出るのだが……?!
※質問された本人より、下記に解答が寄せられました。