えー、2年10組12番というのは、今日の3時までの話で、
クラス替えが、離任式の後にあったんですね。
だから、投稿者の名前が変わりましたので宜しく。
ああ、もう3年か、受験生だな、頑張ろう!!
前置きはここまでにしておいて、質問です。
質問とは言っても、先生が、「知っておくと便利だから。」と紹介程度
で終わりました。でも、具体的に知りたくて、投稿しました。
くだらない質問です。
問1「マクローリン展開」とは、何ですか?
問2
「∞になるスピード」というのは?
後者については、見ただけで(問題を見ただけで)
一瞬で極限が分かるという驚きもの。
ちなみに、
・・・logx・・\(\sqrt{\quad}\)x、x、x2 ・・・ex・・・・
←遅い――――――――――――――――――――速い→
こう教えられただけで、何故∞になるスピードの
速い遅いが分かるのか、そして、そんなものがあったのか?というのを
疑問に思いました。
そして、k>0として、
limx^klogx=0になる。
x→+0
と教えられ、いずれも納得いかずに授業が終了しました。
また何故、上の問題が0に収束するのかがわかりません。
ごちゃごちゃしてすみません。2問ほどですが宜しくお願いします。
数Ⅲって難しいですね。
もう高校3年生ですね。ますます数学の勉強頑張ってください。
問1
マクローリン展開については、質問<89>まち「テイラー展開」のところ
で書いたことを再録します。
=================================
18世紀前半にイギリスで活躍した数学者Brook Taylorが考
えた展開で、
(b-a)2 (b-a)3
f(b)=f(a)+(b-a)f'(a)+── f''(a)+ ── f'''(a)+……
2! 3!
テイラー展開とかテイラー級数とか言う。
関数f(x)が連続で微分可能な区間であれば、テイラー展開が
作れる。
b=x、a=0とすると、
x2 x3
f(x)=f(0)+xf'(0)+── f''(0)+ ── f'''(0)+……
2! 3!
となり、関数f(x)は0の所での導関数で表現できる。
このあたりを詳しく調べたマクローリンの名前をつけて、
マクローリン展開とも言う。一般にテイラー展開という。
例えば、
sinx=x-x3/3!+x5/5!-x7/7!+……
cosx=1-x2/2!+x4/4!-x6/6!+……
ex=1+x/1!+x2/2!+x3/3!+……
log(1+x)=x-x2/2+x3/3-x4/4+……ただし、-1<x≦1
等々である。
いろいろと考えられた関数を一つの形式で表現したかったの
だろうか?または、微積分が考え出されたときなので、使っ
てみたらこうなったのだろうか?動機は分からない。
証明だが、
関数f(x)がべき級数で表現できたとすると、
f(x)=a0+a1x+a2x2+a3x3+a4x4+……
微分して、
f'(x)=a1+2a2x+3a3x2+4a4x3+……
f''(x)=2a2+3・2a3x+4・3a4x2+……
f'''(x)=3・2・1a3+4・3・2a4x+……
ここで、x=0を代入すると、
f(0)=a0
f'(0)=a1
f''(0)=2a2したがって、a2=f''(0)/2!
f'''(0)=3・2・1a3したがって、a3=f'''(0)/3!
べき級数に戻して、
f(x)=f(0)+f'(0)x+f''(0)/2!・x2+f'''(0)/3!・x3+……
となる。出発点はべき級数からであったようだ。
==================================
問2
「∞になるスピード」が分かると、極限が解きやすくなります。
lim f(x)
x→∞
は、関数f(x)の形により、無限になるスピードが違ってきます。
例えば、関数f(x)=x2 と関数f(x)=2xで調べてみましょう。
xに自然数を順に入れていくと
:1→2→3→……→ 10→……→ 100→……→∞
y=x2 :1→4→9→……→ 100→……→10000→……→∞
y=2x :2→4→8→……→1024→……→1267650600228229401496703205376→……→∞
このように同じ無限に行くが、そのスピードが関数により違うことがわかる。
グラフを書いてみると、そのスピードがわかりやすい。
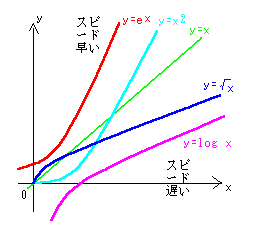
さて極限の問題ですが、
k>0のとき
lim xk ・logx=0
x→+0
ですが、
lim xk =0
x→+0
また、
lim logx=-∞
x→+0
この2つのスピードを比較して考えると、
lim xk ・logx=0・(-∞)=0
x→+0
↑ ↑ ↑
早い 遅い 早い0の勝ち