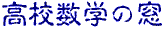私も分かりませんが、ヒントらしきものとして、
重心があります。

ハムの重心を通るように切ると２つに分かれた部分の面積は等しい。
レタスの重心も同様なので、
２つの重心を通るように切れば、問題の趣旨に合う。
しかし、問題はこれにパンが加わり、３つになると
重心が三角形を描くので、包丁で一斬りとはいかない。

※未解決問題に移しますので、どなたかアドバイス下さい。
Toshi Tokudaさんからアドバイスが届きました。
※未解決問題に移したところ、星野さんからも
アドバイスをいただきました。感謝！！

この問題なんですが、僕は学校で「中間値の定理」を使ってやると
聞いたのですが、やり方は忘れてしまいました。
これでは、ヒントにならないですか？

有名な ham sandwich theorem ですが
証明は難しいですね～。
小松あつ郎, 中岡稔, 菅原正博:
位相幾何学 I, 岩波, p. 494 例題 4.8,
中岡稔: 不動点定理とその周辺, 岩波, p. 10 応用例 2.3
ですけれど。

内容は
三次元空間 (\(R^{3}\)) の中に 3 個の有界な可測集合 \(A_{1}\), \(A_{2}\), \(A_{3}\)
(ハムとレタスとサンドイッチ) が与えられたとき, \(A_{1}\), \(A_{2}\), \(A_{3}\) の各々を
等測度に分割するような平面 P が存在する。

証明:
\(R^{3}\) 上にはない \(R^{4}\) の点 \(y_{0}\) を定める。
各 x ∈ \(S^{3}\) (3 次元球面原点中心半径は 1 で考えて良い) に対し, \(Q_{x}\) は
\(y_{0}\) を通り, 直線 Ox (原点と x とを結んだ線) に直交する \(R^{4}\) の超平面
を表すものとする。
￢\(y_{0}\)∈\(R^{3}\) だから, \(Q_{x}\) ≠ \(R^{3}\).
そこで \(Q_{x}\) に関して x + \(y_{0}\) と同じ側にある \(A_{i}\) の部分の測度を \(u_{i}\)(x) で表す。
この時
\(u_{i}\): \(S^{3}\)\(\vec{R}\), i = 1, 2, 3
は連続であるから, 「Borsuk-Ulam の対心点定理」 により,
\(u_{i}\)(a) = \(u_{i}\)(-a)
となる a ∈ \(S^{3}\) が存在する。
各 x ∈ \(S^{3}\) に対し, \(Q_{x}\) = Q_(-x) で, x + \(y_{0}\) と x - \(y_{0}\) は \(Q_{x}\) の反対側
にあるから
\(u_{i}\)(x) + \(u_{i}\)(-x) = m(\(A_{i}\)) (\(A_{i}\) の測度)
が成立する。従って特に
\(u_{i}\)(a) = \(u_{i}\)(-a)= m(\(A_{i}\))/2, i = 1, 2, 3.
\(Q_{a}\) は \(R^{3}\) と平行ではないので, \(Q_{a}\) と \(R^{3}\) の交わりを P とすると
この P が求めるものである□

勿論一般には \(R^{n}\) と \(A_{1}\), ... , \(A_{n}\) で証明出来る。

さて途中で言及した「Borsuk-Ulam の対心点定理」 はこういう内容。

任意の連続写像 f: \(S^{n}\)\(\vec{R}\\()^{n}\) に関し x ∈ \(S^{n}\) が存在して f(-x) = f(x).

今の場合必要なのは n = 3 だからそれに関して説明すると
もしもそういう x ∈ \(S^{3}\) が存在しないとすればそれが矛盾であることを示す。
h: \(D^{3}\)\(\vec{S}\\()^{3}\): (x, y, z)→(x, y, z, \(\sqrt{\quad}\)(1-\(x^{2}\)-\(y^{2}\)-\(z^{2}\)))
\(D^{3}\) = {(x, y, z): \(x^{2}\) + \(y^{2}\) + \(z^{2}\) ≦1}
を用いて
G: \(D^{3}\)\(\vec{S}\\()^{2}\): (f(h(x))-f(-h(x)))/|f(h(x))-f(-h(x))|
g=G|\(S^{2}\) (\(S^{2}\) への制限) と置くと, g は定値写像に homotope だから
deg g = 0. ところが g(-x) = -g(x) だから deg g は奇数でなければならない。
これは矛盾である。

というわけで証明は易しくない。

レタス無しのハムサンドイッチならば,
ご指摘の通り中間値の定理だけで証明出来る。
というのは例えば xy 平面にこれをおいて, z 軸に平行な平面で
パンを二等分する平面を, x 軸との一般角 θ で parameter 表示しておき,
この平面のどちらか一方の決めた側にあるハムの体積を f(θ) で表す。
0 ≦ θ ≦ 2π と考えて良く, f(0) = f(2π) がもとの体積の \(\frac{1}{2}\) ならば
それで終り。
もしそうでなければ f(0) 又は f(2π) のどちらか一方が
もとの体積の \(\frac{1}{2}\) より大きく,
他方がもとの体積の \(\frac{1}{2}\) より小さい (f(θ)+f(2π-θ) が
ハム全体の体積で, f(θ)は正値函数だから)。
この函数に関し中間値の定理を用いればよいわけである。