問1
不等式6X^2+7X-5≦0を解くと、□≦X≦□となる。
同様に、不等式2X^2>5X+12を解くと、X<□、X>□となる。この2つ
の不等式をともに満たすXの値の範囲は、□≦X<□である。
問2
aを定数とするとき、|X|+2|y|=2とy=\(\frac{1}{4}\)X^2-aとの交点の個数を
求めよ。
問3
2次関数f(X)=aX^2-2bX-aを考える。a、bは定数で、a>0とする。
(1)放物線y=f(X)の頂点の座標を求めよ。
(2)f(X)が区間-1≦X≦1で最大値2、最小値-4をとるとき、
a、bの値をもとめよ。
問4
X、yが実数で、X^2+y^2=2Xを満たす時、X+yの最大値と最小値を
求めよ。
問5
(1)Xの2次方程式2k\(X^{2}\)+2(k-1)X+(K+3)=0が相異なる2つの実数解を
もつとき、実数である定数kの値の範囲を求めよ。
(2)2次方程式\(X^{2}\)+X+2=0の2つの解を、α、βとするとき、
(α^2+5α+2)(β^2+7β+2)の値を求めよ。
(3)2次方程式\(X^{2}\)-(m-10)X+m+14=0の異なる2つの実数解がともに負
となるようなmの値の範囲を求めよ。
問6
Aの実数の定数として、Xの方程式
a\(X^{3}\)‐(a+1)\(X^{2}\)-2X+3=0・・・①
の実数解の個数を考える。ただし、重解は1個と考える。
(1)方程式の①の左辺を因数分解せよ。
(2)a=2のとき、方程式①の実数解を求めよ。
(3)方程式①実数解の個数が2個となるとき、aの値と解を求めよ。
問7
(1)等式ab=2a+4b-5を満たす正の整数a、bの組をすべて求めよ。
(2)\(X^{2}\)+6y^2=360を満たす正の整数X、yの値を求めよ。
問8
Xについての2つの2次不等式\(X^{2}\)-2X-8<0
\(X^{2}\)+(4-a)X-4a≧0を同時に満たす整数は、ただ1つであるという。
このとき、aの値の範囲を求めよ。
問1
6x2 +7x-5≦0より、(2x-1)(3x+5)≦0
5 1
∴-―≦x≦―
3 2
2x2 >5x+12
2x2 -5x-12>0より、(2x+3)(x-4)>0
3
∴x<-―,4<x
2
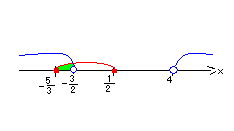
共通部分は
5 3
-―≦x<-― ………(答)
3 2
問2
|x|+2|y|=2のグラフは菱形となる。
x≧0,y≧0のとき、x+2y=2
x≧0,y<0のとき、x-2y=2
x<0,y≧0のとき、-x+2y=2
x<0,y<0のとき、-x-2y=2
1
y=―x2 -aとx-2y=2の接点Aのときのaを求めると、
4
4y=x2 -4a
=(2y+2)2 -4a
4y2 +8y+4-4y-4a=0
4y2 +4y+4-4a=0
y2 +y+(1-a)=0
判別式D=0より、
D=1-4(1-a)=0
1-4+4a=0
4a=3
3
∴a=―
4
1
y=―x2 -aのy切片-aを上から下にずらしながら
4
交点の数を数えていくと、
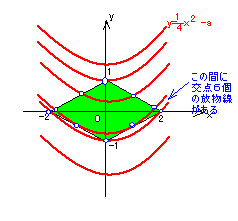
{-a>1のとき、a<-1では、交点は0個
{-a=1のとき、a=-1では、交点は1個
{ 3 3
{1>-a>-―のとき、―>a>-1では、交点は2個
{ 4 4
{
{ 3 3
{-a=-―のとき、a=―では、交点は4個
{ 4 4
{
{ 3 3
{-―>-a>-1のとき、―<a<1では、交点は6個
{ 4 4
{
{-a=-1のとき、a=1では、交点は3個
{-a<-1のとき、a>1では、交点は0個 ………(答)
問3
f(x)=ax2 -2bx-a(ただし、a>0)
平方完成すると、
b a2 +b2
f(x)=a(x-―)2 -―――――
a a
頂点のx座標が次の4つの場合に最大値・最小値の取り方が変わるから、
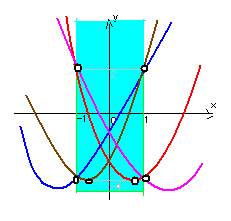
b
―≦-1のとき、最小値f(-1)=-4、最大値f(1)=2
a となるa,bは存在しない。
b b
-1<―≦0のとき、最小値f(―)=-4、最大値f(1)=2
a a
となるa=2\(\pm\)\(\sqrt{\quad}\)3、b=-1
a+b>0より、a=2+\(\sqrt{\quad}\)3、b=-1
b b
0<―≦1のとき、最小値f(―)=-4、最大値f(-1)=2
a a
となるa=2\(\pm\)\(\sqrt{\quad}\)3、b=1
a-b≧0より、a=2+\(\sqrt{\quad}\)3、b=1
b
1<―のとき、最小値f(1)=-4、最大値f(-1)=2
a となるa,bは存在しない。
したがって、
(a,b)=(2+\(\sqrt{\quad}\)3,\(\pm\)1)………(答)
問4
x2 +y2 =2x
(x-1)2 +y2 =1
x+y=kとおくと、
y=-x+k
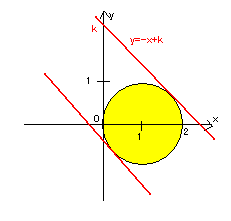
kが最大・最小になるのは、直線と円が接するときだから、
(x-1)2 +(-x+k)2 =1
2x2 -2(1+k)x+k2 =0
判別式D=0より、
D/4=(1+k)2 -2k2 =0
k2 -2k-1=0
k=1\(\pm\)\(\sqrt{\quad}\)2
したがって、
最大値はk=1+\(\sqrt{\quad}\)2
最小値はk=1-\(\sqrt{\quad}\)2………(答)
問5
(1)2kx2 +2(k-1)x+(k+3)=0
が異なる実数解を持つには、判別式D>0より、
D/4=(k-1)2 -2k(k+3)>0
k2 +8k-1<0
k=-4\(\pm\)\(\sqrt{\quad}\)17より、
-4-\(\sqrt{\quad}\)17<k<-4+\(\sqrt{\quad}\)17………(答)
(2)x2 +x+2=0の解をα、βとすると、
α2 +α+2=0より、
α2 +5α+2=(α2 +α+2)+4α=4α
β2 +β+2=0より、
β2 +7β+2=(β2 +β+2)+6β=6β
したがって、
与式=(α2 +5α+2)(β2 +7β+2)
=4α・6β=24αβ
解と係数の関係より、
αβ=2
したがって、
与式=24・2=48………(答)
(3)x2 -(m-10)x+(m+14)=0が異なる実数解を持つから
判別式D>0より
D=(m-10)2 -4(m+14)>0
m2 -24m+44>0
(m-22)(m-2)>0
m<2,22<m
2解がともに負より、α+β<0、αβ>0
解と係数の関係より、
m-10<0∴m<10
m+14>0∴m>-14
したがって、
-14<m<2………(答)
問6
ax3 -(a+1)x2 -2x+3=0
(1)組み立て除法より、
a -(a+1) -2 3 |1
a -1 -3  ̄
―――――――――――――――――
a -1 -3| 0
(x-1)(ax2 -x-3)=0………(答)
(2)a=2のとき、
(x-1)(2x2 -x-3)=0
(x-1)(2x-3)(x+1)=0
3
∴x=1,―,-1………(答)
2
(3)解が2個となるのは、片一方が重解の時だから、
x=1が重解の時、ax2 -x-3=0に代入すると、
a-1-3=0∴a=4
4x2 -x-3=0
(4x+3)(x-1)=0
3
∴x=-―,1
4
したがって、
3
a=4のとき、x=1(重解),x=-―………(答)
4
x=1でない方が重解の時、ax2 -x-3=0が平方式となるから
1 1
ax2 -x-3=a(x-――)2 -――-3
2a 4a
1 1
-――-3=0より、a=-――
4a 12
1
-――x2 -x-3=0
12
x2 +12x+36=0
(x+6)2 =0
∴x=-6(重解)
したがって、
1
a=-――のとき、x=1,x=-6(重解)………(答)
12
問7
(1)ab=2a+4b-5
(a-4)b=2a-5
2a-5 3
b=――――=2+―――
a-4 a-4
bが整数となるから、分母の(a-4)は\(\pm\)1または\(\pm\)3の場合のみ。
a-4=1のとき、a=5、b=5
a-4=-1のとき、a=3、b=-1←これは不適(∵正の整数)
a-4=3のとき、a=7、b=3
a-4=-3のとき、a=1、b=1
したがって、
(a,b)=(5,5)、(7,3)、(1,1)………(答)
(2)x2 +6y2 =360
x2 =360-6y2
=6(60-y2 )
x2 は6の倍数で平方数だから
62 =6(60-y2 )より、
6=60-y2
y2 =54←平方数ではない
122 =6(60-y2 )
24=60-y2
y2 =36
∴y=6
182 =6(60-y2 )
54=60-y2
y2 =6←平方数ではない
したがって、
(x、y)=(12,6)………(答)
問8
x2 -2x-8<0
(x-4)(x+2)<0
∴-2<x<4
x2 +(4-a)x-4a≧0
(x+4)(x-a)≧0
-4≦aのとき、x≦-4,a≦x
a≦-4のとき、x≦a,-4≦x
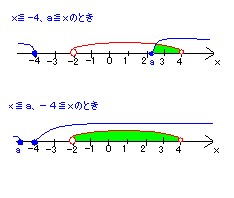
整数が唯1つ答えの範囲にはいるのは、aの範囲が次の時である。
2<a≦3………(答)