π
－―＜θ＜０
　２
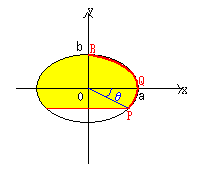
楕円より、
｛ｘ＝ａcosφ
｛ｙ＝ｂsinφ
　　　　π
θ≦φ≦―の範囲で弧ＰＱＲを描く。
　　　　２

弧ＰＱＲをｙ軸の周りに回転させてできる体積は
ｂ
∫　πｘ² ｄｙ
bsinθ

　　π/2
＝π∫　ａ² cos² φ・ｂcosφｄφ
　　θ

　　　　　π/2
＝πａ² ｂ∫　cos³ φｄφ
　　　　　θ

　　　　　１
＝πａ² ｂ∫　（１－ｔ² ）ｄｔ
　　　　　sinθ

　　　　　　２　　　　　１
＝πａ² ｂ（―－sinθ＋――sin³ θ）＝（※１）
　　　　　　３　　　　　３

３倍角の公式を利用して、
　　　　　　　　　　２　３　　　　　１
（※１）＝πａ² ｂ（―－―sinθ－―――sin３θ）………（答）
　　　　　　　　　　３　４　　　　１２

弧ＰＱＲが描く表面積は、底の部分は除くと、
ｂ　　　　　　　ｄｘ　　　ｄｙ
∫　２πｘ\(\sqrt{\quad}\)｛（――）² ＋（――）² ｝ｄφ＝（※２）
bsinθ　　　　　ｄφ　　　ｄφ
ｄｘ
――＝－ａsinφ
ｄφ

ｄｙ
――＝ｂcosφ
ｄφ

　　　ｄｘ　　　ｄｙ
\(\sqrt{\quad}\)｛（――）² ＋（――）² ｝
　　　ｄφ　　　ｄφ

＝\(\sqrt{\quad}\)（ａ² sin² φ＋ｂ² cos² φ）

　　　　ａ²
＝ｂ\(\sqrt{\quad}\)（――sin² φ＋cos² φ）
　　　　ｂ²

　　　　ａ²
＝ｂ\(\sqrt{\quad}\)｛――sin² φ＋（１－sin² φ）｝
　　　　ｂ²

　　　　　　ａ² －ｂ²
＝ｂ\(\sqrt{\quad}\)（１＋―――――sin² φ）＝（※３）
　　　　　　　　ｂ²

ａ² －ｂ²
―――――＝ｅ² とおくと、
　　ｂ²

（※３）＝ｂ\(\sqrt{\quad}\)（１＋ｅ² sin² φ）

　　　　　　　π/2
（※２）＝２π∫　ａcosφ・ｂ\(\sqrt{\quad}\)（１＋ｅ² sin² φ）ｄφ
　　　　　　　θ

　　　　　　　　　π/2
　　　　＝２πａｂ∫　\(\sqrt{\quad}\)（１＋ｅ² sin² φ）・cosφｄφ
　　　　　　　　　θ

　　　　　　　　　１
　　　　＝２πａｂ∫　\(\sqrt{\quad}\)｛１＋（ｅｔ）² ｝ｄｔ
　　　　　　　　　sinθ

　　　　　２πａｂ　ｅ
　　　　＝――――・∫　\(\sqrt{\quad}\)（１＋ｚ² ）ｄｚ
　　　　　　ｅ　　　ｅsinθ

　　　　　２πａｂ　１　　　　　　　　　　　　　　　　　　　　　　　　ｅ
　　　　＝――――・―［ｚ\(\sqrt{\quad}\)（ｚ² ＋１）＋１・log｜ｚ＋\(\sqrt{\quad}\)（ｚ² ＋１）｜］
　　　　　　ｅ　　　２　　　　　　　　　　　　　　　　　　　　　　　　ｅsinθ

　　　　　πａｂ
　　　　＝―――｛ｅ\(\sqrt{\quad}\)（ｅ² ＋１）＋log｜ｅ＋\(\sqrt{\quad}\)（ｅ² ＋１）｜
　　　　　　ｅ

　　　　　－ｅsinθ\(\sqrt{\quad}\)（ｅ² sin² θ＋１）－log｜ｅsinθ＋\(\sqrt{\quad}\)（ｅ² sin² θ＋１）｜｝………（答）