(1)3x+2y=12のとき、xyの最大値をもとめよ。
(2)点(-3,1)を通り、円x^2+y^2=1に接す
る直線の方程式の中で、x軸に平行出ない直線は( )で
あり、その接点の座標は( )である。
(3)x(x-2)/3+x/6≦1-x/8-x/6を満
足するxの値の範囲は( )≦x≦( )である。
(4)a>b>0のとき、1<a+1/b+1<a/bを証
明しなさい。
(5)和が3,積が1になる2つの数のなかで、大きい方の
数は( )である。
問(1)
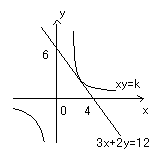
3x+2y=12を変形して、y=-\(\frac{3}{2}\)x+6
xy=kに代入して
-\(\frac{3}{2}\)x2+6x=k
3x2-12x+2k=0
判別式よりD=144-24k≧0
k≦6
したがってkの最大値は6……(答)
問(2)
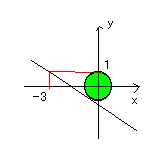
接点P(a,b)とすると、
接線の公式より、ax+by=1
この接線が点(-3,1)を通るから、-3a+b=1
変形してb=3a+1……①
円周上より、a2+b2=1……②
①を②に代入して、a2+(3a+1)2=1
変形して、10a2+6a=0
∴a=0,-3/5
接線はx軸に平行でないので、a=-3/5
①に代入して、b=-4/5
接点P(-3/5,-4/5)……(答)
接線ax+by=1に代入して
-\(\frac{3}{5}\)x-\(\frac{4}{5}\)y=1
変形して、y=-\(\frac{3}{4}\)x-\(\frac{5}{4}\)……(答)
問(3)
両辺に24を掛けて8x(x-2)+4x≦24-3x-4x
変形して
8x2-5x-24≦0
方程式の解の公式より
x=(5\(\pm\)\(\sqrt{\quad}\)793)/16
二次不等式の解の範囲は
(5-\(\sqrt{\quad}\)793)/16≦x≦(5+\(\sqrt{\quad}\)793)/16
問(4)
①1<(a+1)/(b+1)の証明
a>b>0より、a+1>b+1>1>0
b+1>0で割って、
(a+1)/(b+1)>1
②(a+1)/(b+1)<a/bの証明
a>b>0より、a+1>b+1>1>0
a>b>0より、ab>0
両辺に加えて
a+ab>b+ab
a(1+b)>b(1+a)
b+1>0、b>0で割って、
a/b>(1+a)/(1+b)
したがって①②より証明できた。
問(5)
解と係数の関係より
和α+β=3、積αβ=1より、
t2-3t+1=0
解の公式より
t=(3\(\pm\)\(\sqrt{\quad}\)5)/2
∴(3+\(\sqrt{\quad}\)5)/2……(答)