質問＜１８４＞の問２と同じ問題ですね。

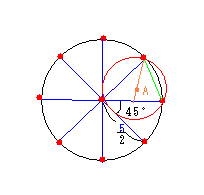
９個の点は距離２より大きな場所において、１０番目の点がどこにおいても
距離２より小さくなることを示す。
これを「The Pigeonhole Principle（鳩小屋の穴の原理）」と言う。

正８角形の１辺の長さは、質問＜１２３１＞と同じ余弦定理より、
ｘ^2＝（５／２）^2＋（５／２）^2－２・（５／２）・（５／２）cos４５°
　　＝２５／２－（２５／２）・（１／\(\sqrt{\quad}\)２）
ｘ＞０より、
∴ｘ＝\(\sqrt{\quad}\)｛２５／２－（２５／２）・（１／\(\sqrt{\quad}\)２）｝
　　＝1.913417161825448858642299920152
　　　（電卓により）
　　≒１．９１

１つの三角形の外接円の中心Ａからの半径Ｒを計算すると、
正弦定理より、
１．９１
――――＝２Ｒ
sin４５°

　　　　１．９１　　　１．９１
Ｒ＝――――――――＝――――＝1.3505739520663057716056127316203
　　２・（１／\(\sqrt{\quad}\)２）　　\(\sqrt{\quad}\)２

　≒１．３５＜２
したがって、
１０番目の点はどこにとっても、２点間の距離が２より小さくなる。

「９個の点は距離２より大きな場所において」の意味を詳しく
教えて下さい。

確かに、距離２より大きな９つの点は取れませんね。
上のｘ＝１．９１＜２ですから。
そうすると、はじめの５つの点は距離２より大きくとれるが、
残りの５つの点は、必ず最初の５点のどれかとの距離は、
２より小さくなりますね。
証明はどう考えればよいのでしょうか？

座標平面の原点を中心とし、直径5,2の円をそれぞれC,D,
直線x=0,y=0,x=y,x=-yをそれぞれp,q,r,sとして、
Cの内部を、Dの内部と、CとDの間をp,q,r,sで分割したものの
計9個の領域に分けるとよいでしょう。（Dの周は、外側の領域に含める）

"Pigeonhole Principle"には、「鳩の巣(箱の)原理」という定訳が
あります。
質問の趣旨とは全く関係ありませんが、ちょっと気になったので。