質問

今年から高校に入学するのですが、春休みの課題がどうして
もわからなくて困っています。お願いします、おしえてくだ
さい！

【１】
交わる２つの円の交点を通る直線上に点Ｐをとり、Ｐから
２つの円に接線をひいたとき、Ｐから接点までの長さはす
べて等しいことを示せ。

【２】
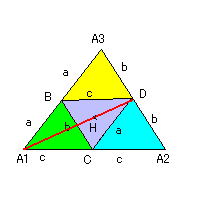
△ＡＢＣの外心をＯとする。直線ＢＣ、ＣＡ、ＡＢについ
て、Ｏの対称点をそれぞれＡ’、Ｂ’、Ｃ’とするとき、
次の問に答えよ。
　　　　（１）△ＡＢＣ≡△Ａ’Ｂ’Ｃ’を示せ。
　　　　（２）Ｏは△Ａ’Ｂ’Ｃ’の外心、内心、重心、垂心の
　　　　　　　いずれか。理由を付けて答えよ。

【３】
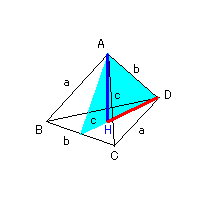
四面体ＡＢＣＤがある。ＡＢ＝ＣＤ＝ａ、ＡＤ＝ＢＣ＝ｂ、
ＡＣ＝ＢＤ＝ｃのとき、この四面体の体積をａ、ｂ、ｃを用
いて表せ。

【４】
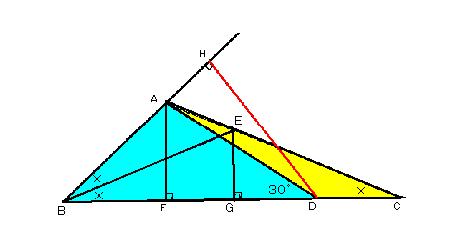
△ＡＢＣにおいて、∠Ｂ＝２∠Ｃとする。辺ＢＣ上に点Ｄを
ＢＤ＝ＡＣにとるとき、∠ＡＤＢ＝３０°ならば、∠Ｃは何
度か。

【５】
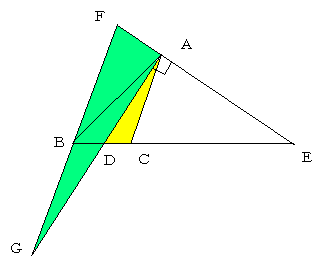
△ＡＢＣの辺ＢＣの上の点をＤ、辺ＢＣの延長上の点をＥと
する。
ＢＤ：ＤＣ＝ＢＥ：ＥＣ、∠ＤＡＥ＝９０°ならば、
∠ＢＡＤ＝∠ＣＡＤであることをを示せ。

こんなにたくさんごめんなさい。よろしくお願いします。

お返事９９／４／１０
from=武田

最近質問が無くて、のんびりしていてこのメールに気づいた
のが７日の夜の１１時過ぎです。早速解いてみましたが、全
然解けないのに愕然としました。
プリントに印刷して、その後持ち歩きながら、高校の始業式
や入学式をこなしていきました。年度始めはやたらと仕事が
あるので、なかなか解く暇がありませんでしたし、またなか
なか解けませんでした。
解けない理由を考えてみました。全部の問題が図形に関する
問題で、それもユークリッドやアルキメデス達が活躍した時
代の公式や定理を利用する問題だったからです。日本でも戦
前の頃などには、教科書にも「幾何」という題目で勉強して
いました。現代の教科書は「関数」など図形と言うよりグラ
フ中心に勉強が展開されていますので、私もすっかり失念し
てしまっていたのです。
どなたか分からない所を補って下さい。

【１】

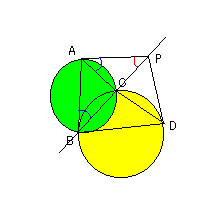
△ＰＡＢと△ＰＡＣにおいて、∠ＡＰＢ＝∠ＡＰＣ（共通）
接弦定理より∠ＰＢＡ＝∠ＰＡＣ
∴△ＰＡＢ∽△ＰＡＣ
比より、ＡＰ：ＰＢ＝ＰＣ：ＡＰ
ＰＢ・ＰＣ＝ＡＰ²……①
△ＰＢＤと△ＰＤＣにおいても同様にして、
ＰＢ・ＰＣ＝ＤＰ²……②
①と②より
ＡＰ²＝ＤＰ²
∴ＡＰ＝ＤＰ
したがって、Ｐから接点までの長さはすべて等しい。

【２】

外心なので、Ｏを中心とした円は△ＡＢＣの外接円となる。
Ｏに関する点対称なので、Ａ’、Ｂ’、Ｃ’はすべて円周上
にある。したがって、（２）は△Ａ’Ｂ’Ｃ’も外接円の中
にあるので、外心となる。
（１）は、△ＡＢＯと△Ａ’Ｂ’Ｏにおいて、ＯＡ＝ＯＡ’
ＯＢ＝ＯＢ’、∠ＡＯＢ＝∠Ａ’ＯＢ’なので、２辺とその
間の角が等しいので、△ＡＢＯ≡△Ａ’Ｂ’Ｏ
したがって、ＡＢ＝Ａ’Ｂ’……①
同様にして、△ＢＣＯ≡△Ｂ’Ｃ’Ｏより、
ＢＣ＝Ｂ’Ｃ’……②
同様にして、△ＡＣＯ≡△Ａ’Ｃ’Ｏより、
ＡＣ＝Ａ’Ｃ’……③
①②③より３辺が等しいので、
△ＡＢＣ≡△Ａ’Ｂ’Ｃ’

【３】

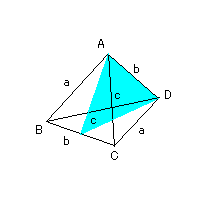
未だ出来ず！なにか公式があるのかも？

【４】

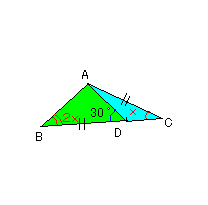
未だ出来ず！どこかに補助線を引くのかも？

【５】

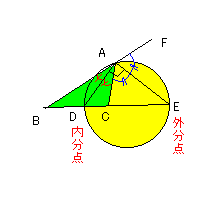
大昔のアポロニウスが見つけた「アポロニウスの円」に関す
る問題であったが、解法は分からない。
内分点Ｄと外分点Ｅを直径とする円上の点Ａにおいて、
内角∠ＢＡＣと外角∠ＣＡＦのそれぞれの二等分線がＡＤ、
ＡＥとなる。（定理）
上の定理より、∠ＢＡＣの二等分線がＡＤより、
∴∠ＢＡＤ＝∠ＣＡＤ

お便り９９／５／２５
from=関谷敏雄

　先日はご苦労様でした。さっそくホームページを見させて
もらいました。すばらしいホームページですね。私も数学の
質問に答えるホームページを作りたくなりました。
　さて、質問や解答の紹介コーナーを見ていて、結構難しい
問題があるな、と思いましたが、その中の１つを解いてみて、
自分なりの解答が得られましたので、メールさせていただき
ます。

＜問４＞
　△ＡＢＣにおいて、∠Ｂ＝２∠Ｃとする。辺ＢＣ上に点Ｄ
をＢＤ＝ＡＣにとるとき、∠ＡＤＢ＝３０°ならば、∠Ｃは
何度か。

初等幾何を用いた解答
（方針）∠ＡＤＨ＝ｘとなることを目標にする。
（解）

△ ＢＤＨ∽△ＢＡＦより、ＤＨ／ＢＤ＝ＡＦ／ＡＢ
　∴ＤＨ＝ＡＦ・ＢＤ／ＡＢ
両辺をＡＤで割って
　ＤＨ／ＡＤ＝（ＡＦ／ＡＤ）・（ＢＤ／ＡＢ）
　　　　　　＝（１／２）・（ＢＤ／ＡＢ）
　　　　　　＝（１／２）・（ＡＣ／ＡＢ）
　　　　　　＝（１／２）・（ＡＢ／ＡＥ）
　　　　　　　　　　　　　　（　△ＡＢＣ∽△ＡＥＢより）
　　　　　　＝（１／２）・（ＢＣ／ＣＥ）
　　　　　　　　　　　　　　（角の二等分線の性質より
　　　　　　　　　　　　　　　　ＢＡ：ＢＣ＝ＡＥ：ＣＥ）
　　　　　　＝（１／２）・（２ＣＧ／ＣＥ）
　　　　　　＝ＣＧ／ＣＥ
△ ＡＤＨと△ＥＣＧは、直角三角形で、２組の対応する辺の
比が等しくなるので、相似である。よって、∠ＡＤＨ＝ｘ。
△ＢＤＨの内角の和は１８０度だから、
２ｘ＋（３０°＋ｘ）＋９０°＝１８０°
３ｘ＝６０°
　ｘ＝２０°
よって、∠Ｃ＝２０°である。（以上）

三角比の正弦定理を用いるともっと、易しくなります。
（解）△ＡＢＤに正弦定理を用いて
ＢＤ／ｓｉｎ∠ＢＡＤ＝ＡＤ／ｓｉｎ２ｘ　…①
△ ＡＤＣに正弦定理を用いて
ＡＣ／ｓｉｎ１５０°＝ＡＤ／ｓｉｎｘ　　…②
②÷①により
ｓｉｎ∠ＢＡＤ／ｓｉｎ１５０°＝ｓｉｎ２ｘ／ｓｉｎｘ
　　　　　　　　　　　　　　　　　（仮定よりＡＣ＝ＢＤ）
ｓｉｎ∠ＢＡＤ＝ｓｉｎ２ｘｓｉｎ１５０°／ｓｉｎｘ
　　　　　　　＝２ｓｉｎｘｃｏｓｘ・（１／２）／ｓｉｎｘ
　　　　　　　＝ｃｏｓｘ
∠ＢＡＤ＝１８０°―３０°―２ｘ＝１５０°－２ｘ　より
ｓｉｎ（１５０°―２ｘ）＝ｃｏｓｘ
ｃｏｓ（６０°―２ｘ）＝ｃｏｓｘ
∴６０°―２ｘ＝ｘ
∴ｘ＝２０°
よって、∠Ｃ＝２０°

お便り９９／６／２
from=関谷敏雄

　武田先生、こんにちは。先日は、メールで送った解答を
ＨＰに掲載していただき、（しかも綺麗な図までつけて）、
ありがとうございました。同じ「春休みの課題」の中の
四面体の体積を求めましたので、送らせていただきます。
（武田談：送っていただいた内容を若干表現し直して下記に
記させてもらいます。）


四面体の頂点Ａをもって切り開くと、

となる。
四面体の頂点Ａから△ＢＣＤに下ろした垂線の足は、展開し
た△Ａ₁Ａ₂Ａ₃の垂心Ｈになるから、
座標を導入して、垂心Ｈの座標やＤＨの長さや四面体の高さ
ＡＨの長さを求め、最後に四面体の体積Ｖを求めるとよい。

座標Ａ₁（ｓ，０）
座標Ａ₂（ｔ，０）
座標Ａ₃（０，ｒ）とおくと、
垂心Ｈ（０，－ｓｔ／ｒ）
座標Ｄ（ｔ／２，ｒ／２）より、
（ＤＨの長さ）²＝ｔ²／４＋（ｒ／２＋ｓｔ／ｒ）²
（高さＡＨ）²＝ｂ²－（ＤＨ）²
△ＢＣＤの面積＝１／２・ｒ／２・（ｔ／２－ｓ／２）
したがって、
四面体の体積Ｖ＝１／３・△ＢＣＤ・ＡＨ
＝＝途中の計算は省略＝＝
∴ａ²＋ｂ²＋ｃ²＝２ｓとおくと、
Ｖ＝１／３√｛（ｓ－ａ²）（ｓ－ｂ²）（ｓ－ｃ²）｝

（武田談：とっても素敵な答になりました。公式になりそう
な気がします。ヘロンの公式の立体版ですね。
関谷先生有り難うございました。）

お便り２００１／１１／９
from=CharlieBrown

こんばんは。
いつも素早い対応、ありがとうございます。
今回はかなり昔の問題で別解を見つけたので、
そちらの紹介をしたいと思います。

問題は、
四面体ＡＢＣＤがある。ＡＢ＝ＣＤ＝ａ、ＡＤ＝ＢＣ＝ｂ、
ＡＣ＝ＢＤ＝ｃのとき、この四面体の体積をａ、ｂ、ｃを用
いて表せ。
というものでした。
座標を用いた解答が関谷氏から寄せられていました。

対角線の長さがそれぞれa、b、cとなる長方形を用意し、
それらを用いてできる直方体APBQ-RCSD から、
4つの四面体 P-ABC、Q-ABD、R-ACD、S-BCD を切り取ると、
残った図形が問題に与えられた四面体ABCDになります。直方体の3辺の長さを、
AP = d、AQ = w、AR = h とおくと、三平方の定理から、
　a^2 =       d^2 + h^2
　b^2 = w^2       + h^2
　c^2 = w^2 + d^2
となります。これを w^2、d^2、h^2 について解くと、
　w^2 = (-a^2 + b^2 + c^2)/2
　d^2 = ( a^2 - b^2 + c^2)/2
　h^2 = ( a^2 + b^2 - c^2)/2
です。求める体積は、直方体の体積から4つの四面体の体積を引けば良いので、
　V = wdh - 4×(wdh/6)
　    1
　  = -wdh
　    3
　    1   -a^2 + b^2 + c^2  a^2 - b^2 + c^2  a^2 + b^2 - c^2
　  = -√{----------------・---------------・---------------}
　    3           2                2                2
となります。これは関谷氏の解答と一致します。

この立体は4面が合同な三角形からできていますが、
そのうちの一つである三角形ABCの3辺の長さ a、b、c の対角を、
改めてA、B、C と名づけ直します。
これは数学Iの三角比で扱う名づけ方に対応させたわけです。
さて、求めた体積を3辺の積で割ると、
　 V    1   -a^2 + b^2 + c^2  a^2 - b^2 + c^2  a^2 + b^2 - c^2
　--- = -√{----------------・---------------・---------------}
　abc   3          2bc              2ca              2ab
　      1
　    = -√{cosA・cosB・cosC}    (∵余弦定理)
　      3
　　    abc
∴　V = ---√{cosA・cosB・cosC}
　       3

この式から次のことがわかります。
三角形ABCが直角三角形だと、
3つのcosの積のうちどれか1つが0になります。
これは、そのような立体を作ることができないことを意味します。
関谷氏の解答の展開図を直角三角形で描いてみるとわかりますが、
例えば∠C が直角の時、CDで折り返して点A2を点A3と合わせるためには、
点A3まで180°折らなければなりません。これでは立体になりません。

同様に、三角形ABCが鈍角三角形でも、
3つのcosの積のうちどれか1つが負になります。
これも、そのような立体を作ることができないことを意味しています。
関谷氏の解答にあるように、
展開図で四面体の頂点Aから底面に下ろした垂線の足が、
三角形A1A2A3の垂心になるわけですから、
3つの折り目 BC、CD、DB で折って1点Aに集めるためには、
この垂心が三角形の内部にある必要があります。
しかし、直角三角形では、垂心は直角の頂点に、
鈍角三角形では、垂心は鈍角の外側に位置しますから、
やはりこれらは四面体に成り得ないわけです。

最後に、正四面体では、a=b=c、cosA=cosB=cosC=1/2 ですから、
　V = (√2/12) a^3
という公式が得られます。

お便り９９／６／６
from=関谷敏雄


　春休みの課題の５のアポロニウスの円の軌跡に関する問題
の証明を与えました。高校１年生のときに授業で習った問題
です。当時はまだ初等幾何が教育課程にありました。私がそ
の教育課程の最後の学年だったと思います。
　一般に軌跡の問題では、逆の証明を与えなければなりませ
ん。逆の証明は、元の証明の道筋を逆にたどることによって
得られることが多いのですが、アポロニウスの円では逆の証
明がそう簡単ではないと先生に教わりました。（曖昧な記憶
ですが）
　有名な問題ですから，初等幾何の何かの本には載っている
でしょうが、私の手元にはそのような本がありません（教科
書にはあるのでしょうか？初等幾何は全然授業ではやらない
ので気がつきませんでしたが）。もし、そういう本をご存知
でしたら，教えて下さい。
【証明】

ＡＣに平行な点Ｂを通る直線を引き、直線ＥＡの延長との交
点をＦ、直線ＡＤの延長との交点をＧとする。
ＡＣとＦＢが平行だから、△ＥＦＢ∽△ＥＡＣ。
よって、ＦＢ：ＡＣ＝ＢＥ：ＥＣ
ＡＣとＢＧが平行だから、△ＤＢＧ∽△ＤＣＡ。
よって、ＢＧ：ＡＣ＝ＢＤ：ＤＣ
仮定より、ＢＥ：ＥＣ＝ＢＤ：ＤＣだから、
ＦＢ：ＡＣ＝ＢＧ：ＡＣ。
よって、ＦＢ＝ＢＧ。
さらに、∠ＦＡＧ＝∠Ｒだから、ＦＢ＝ＢＧ＝ＡＢ。
△ＢＧＡが二等辺三角形だから、∠ＢＡＤ＝∠ＢＧＤ。
∴∠ＢＡＤ＝∠ＣＡＤ