複素数関数は大学で学ぶので、私には難しすぎます。しかし、
答えられないのも悔しいので、コンピュータで作図を試みま
した。すると下図のようになりました。

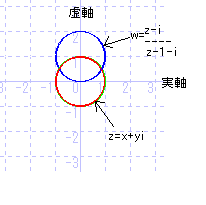
ｚ＝１のとき、ｗ＝１＋ｉ
左向きに単位円上を回転しながらｚ＝ｉに近づくと、
ｗはｉを中心とした半径１の円を描きながら左側から０に近
づいていく。
さらに、ｚが－１に近づいていくと、ｗは\(\frac{3}{5}\)+\(\frac{1}{5}\)iに近づき、
ｚが－ｉに近づくと、ｗは\(\frac{4}{5}\)+\(\frac{2}{5}\)iに近づき、ｚが１に戻る
と、ｗは１＋ｉに戻る。ｗの円は左回転で描き、スピードは
はじめ大きく、あとほど小さくなります。
上の軌跡は、ソフト「十進ＢＡＳＩＣ」のプログラムの中に
あった複素数のを利用しました。

ｗの絶対値は原点からの距離だから、最大値はｗ＝２ｉのと
ころである。ｚ＝\(\frac{4}{5}\)+\(\frac{3}{5}\)i　のとき、｜ｗ｜＝２……（答）

帰りの車の中で、途中までした話の続きです。
途中で終わって、気がかりなので、筆を執りました。
（武田談：学習会の帰りの車の中で、話題になったものを
手紙に書いて送ってくれました。レポート用紙４枚に及ぶ
ものですが、ｗが円とは予想つかないのを前提にした方の
　　　　　　^^^^^^^^^^^^^^^^^^^^^^
内容を要約して掲載します。有り難うございました。）

なお、この質問の一般形
　　ａｚ＋ｂ
ｗ＝────
　　ｃｚ＋ｄ
（ａｄ－ｂｃ≠０）は、１次変換またはメビウス変換といい、
これは、円円対応の性質があることを初めに紹介しておく。

さて、まず与えられた変換の逆変換を考える。
　　（１＋ｉ）ｗ－ｉ
ｚ＝────────
　　　　　ｗ－１

　　　　　　　　　　　　＿
　｛（１＋ｉ）ｗ－ｉ｝（ｗ－１）
　＝───────────────
　　　　　　　　　＿
　　　（ｗ－１）（ｗ－１）

　　　　　　　＿　　　　　＿
　（１＋ｉ）ｗｗ－ｉ（ｗ＋ｗ）－ｗ＋ｉ
　＝─────────────────
　　　　　＿　　　　＿
　　　　ｗｗ－（ｗ＋ｗ）＋１

ここで、ｚ＝ｘ＋ｉｙ、ｗ＝ξ＋ｉηとおく。
両辺の実部と虚部を比較して、
　　　ξ²＋η²－ξ
ｘ＝──────────
　　ξ²＋η²－２ξ＋１

　　　ξ²＋η²－２ξ－η＋１
ｙ＝─────────────
　　ξ²＋η²－２ξ＋１

ここで、分母のξ²＋η²－２ξ＋１≠０に注意する。
　　　　　　　　＝（ξ－１）²＋η²

ｘ²＋ｙ²＝１に代入する。分母を払えば、
（ξ²＋η²－ξ）²＋（ξ²＋η²－２ξ－η＋１）²＝（ξ²＋η²－２ξ＋１）²
ここで、ξ²＋η²－２ξ＋１＝Ａ(≠０）とおけば、
｛Ａ＋（ξ－１）｝²＋（Ａ－η）²＝Ａ²
Ａ²＋（２ξ－２η－２）Ａ＋（ξ²－２ξ＋１＋η²）＝０
Ａ²＋（２ξ－２η－１）Ａ＝０
Ａ≠０で両辺を割って、
Ａ＋（２ξ－２η－１）＝０
ξ²＋η²－２ξ＋１＋（２ξ－２η－１）＝０
ξ²＋η²－２η＝０
ξ²＋（η－１）²＝１
軌跡の点は、中心ｉ、半径１の円周上にあることが分かる。
この逆も言える（省略）ので、
ｗの軌跡は｜ｗ－ｉ｜＝１である。

　武田先生こんばんは。先日はごていねいなメールをありが
とうございました。私の方のＨＰにはまだまだ訪ねてくれる
人が少なく、あちこちのネットで宣伝してまわっているとこ
ろです。これからもよろしくお願いします。
　さて、質問１３５については、以前先生のホームページに
出たときに解答を考えていました。メールを出すタイミング
を逸してしまいまして、今更蛇足になりますが、コメントさ
せていただきます。
　なお、村嶋健吾先生の解答でも指摘されていますが、1次
分数変換では円は円に対応します。それについては、以下の
ような本が参考になります。

　高木貞治　著　「代数学講義　改定新版」
　　　　　　　　　共立出版　第1章　§４～６
　梅沢敏夫・後藤達生　共著　「複素数と幾何学」
　　　　　　　　　培風館　6章　円々変換

　「代数学講義」の方が説明は丁寧だと思いますが、「複素
数と幾何学」の方が簡潔で、短時間で調べ上げるにはそちら
の方が良いと思います。また、「複素数と幾何学」の方は、複素平面を用いて豊富な幾何の解説をしています。私は他に
この様な本を見たことがありません。ご参考までに。

　質問１３５に対する１つの解答例

w = ( z - i ) / ( z - 1 - i ) より
z = { ( 1 + i ) w - i } / ( w - 1 )

| z | = 1 　に代入して
| { ( 1 + i ) w - i } / ( w - 1 ) | = 1
| ( 1 + i ) w - i | = | w - 1 |
| ( 1 + i ) w - i |² = | w - 1 |²
　　　　　　　　　　＿＿＿＿＿＿＿＿　　　　　　　　＿＿＿
｛（１＋i)ｗ－ｉ｝｛（１＋ｉ）ｗ－ｉ｝＝（ｗ－１）（ｗ－１）
　　　　　　　　　　　　　　　＿　　　　　　　　　　＿
｛（１＋i)ｗ－ｉ｝｛（１－ｉ）ｗ＋ｉ｝＝（ｗ－１）（ｗ－１）

これを整理して、
　＿　　　　＿
ｗｗ＋ｗｉ－ｗｉ＝０
　＿　　　　＿
ｗｗ＋ｗｉ－ｗｉ＋１＝１
　　　　　　＿
（ｗ－ｉ）（ｗ＋ｉ）＝１
　　　　　　＿＿＿
（ｗ－ｉ）（ｗ－ｉ）＝１

| w - i |<sup>2
| w - i | = 1

よって、w　の動く軌跡は　i　を中心とした半径１の円。
ｗの絶対値の最大値は２でそのとき w = 2i 。
1行目の式に代入して、z = \(\frac{4}{5}\) +\(\frac{3}{5}\) i</sup>