はじめまして。
数学からかなり遠ざかっていたため、基本的な問題の
ような気がするのですがどうしても解けません。
手元に資料もないので困っています。
お答えいただければ幸いです。
問題1.対角線が直交する台形ABCDにおいて、
BD=a、高さhとするとき、この台形の
面積を求めよ。
問題2.ax^2+bx+c=0(a≠0)の
解の公式を導け。
問題3.長軸が2a、短軸が2bの楕円の面積を求めよ。
問題4.x^2-y^2=1(-2≦y≦2)をy軸を
中心に回転させてできる図形の体積を求めよ。
問1
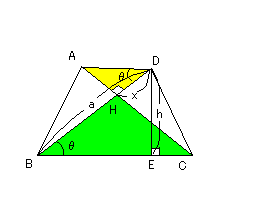
AD//BCより、∠ADH=∠CBH=θ
BD=aをBHとDHに分け、DH=xとおくと、
BH=a-x
△ADHにおいて、cosθ=DH/ADより、
AD=DH/cosθ
=x/cosθ……(1)
△CBHにおいて、cosθ=BH/CBより、
CB=BH/cosθ
=(a-x)/cosθ……(2)
台形の面積は
S=(上底+下底)×高さ÷2
=(AD+CB)×h÷2
=ah/(2cosθ)……(3)
また、△DBEにおいて、
sinθ=DE/BD=h/a……(4)
sin2θ+cos2θ=1に(4)を代入
cosθ=\(\sqrt{\quad}\)(a2-h2)/a……(5)
(5)を(3)に代入すると、
S=a2h/{2\(\sqrt{\quad}\)(a2-h2)}……(答)
問2
平方完成を使って、解の公式を導くと、
a{x2+(b/a)x+(b2/4a2)-(b2/4a2)}+c=0
a(x+b/2a)2-(b2/4a)+c=0
a(x+b/2a)2-(b2-4ac)/4a=0
a(x+b/2a)2=(b2-4ac)/4a
(x+b/2a)2=(b2-4ac)/4a2
平方根を取って、
x+b/2a=\(\pm\)\(\sqrt{\quad}\)(b2-4ac)/2a
x=-b/2a\(\pm\)\(\sqrt{\quad}\)(b2-4ac)/2a
={-b\(\pm\)\(\sqrt{\quad}\)(b2-4ac)}/2a……(答)
問3

楕円の方程式
x2/a2+y2/b2=1を変形して
y=\(\pm\)(b/a)\(\sqrt{\quad}\)(a2-x2)
楕円の四半分の面積を定積分を用いて求め、4倍する。
S=4∫0a(b/a)\(\sqrt{\quad}\)(a2-x2)dx
x=acosθとおいて置換積分をする。
dx=-asinθdθ
x: 0 → a
θ:90°→ 0°
\(\sqrt{\quad}\)(a2-x2)=asinθ
より、
S=4b/a∫π/20asinθ×(-asinθ)dθ
=4b/a∫0π/2a2sin2θdθ
=4ab∫0π/2sin2θdθ
=4ab∫0π/2{(1-cos2θ)/2}dθ
=2ab[θ-sin2θ/2]0π/2
=2ab{(π/2-0)-(0-0)}
=πab……(答)
問4
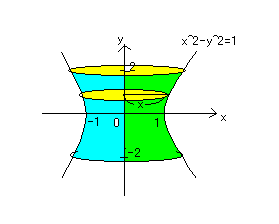
x2-y2=1を変形して、
x2=y2+1
より、
y=-2から2までのy軸の回りの回転体の体積は
V=2×π∫02x2dy
=2π∫02(y2+1)dy
=2π[y3/3+y]02
=2π{(8/3+2)-(0+0)}
=2π×14/3
=(28/3)π……(答)