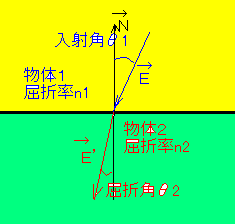
屈折前のベクトルE(単位ベクトル)
法線ベクトルN(単位ベクトル)
物体1の屈折率n1、2の屈折率n2
上記4要素を用いて
屈折後のベクトルE'を求める。
スネルの法則により
n1・sinθ1 = n2・sinθ2
θ1...入射角
θ2...屈折角
cosθ1 = -E ・N
cosθ2 = -E'・N
sinθ1 = | E + Ncosθ1 |
sinθ2 = | E'+ Ncosθ2 |
E,E'は同方向なので絶対値記号"|"を外せる。
上記法則に代入しE'について整理すると、
E' =
(n\(\frac{1}{n}\)2)( E - N(\(\sqrt{\quad}\)((n\(\frac{2}{n}\)1\()^{2}\)-1+co\(s^{2}\)θ1)-cosθ1))
=
(n\(\frac{1}{n}\)2)( E - N(n・cosθ2-cosθ1) )
と変形することができる。
と、とある書籍には掲載されているのですが、
冒頭にある4要素のみでここまで変形させることが
できず困っています。
cosθ2の扱いをどうにか変形できればと思い
公式集も隅々まで調べたのですが手がかりは得られま
せんでした。
何か特殊な変形方法があるのでしょうか?
sinθ2 = | E'+ Ncosθ2 |より、
絶対値記号がとれて、
sinθ2 = E'+ Ncosθ2
E'=sinθ2- Ncosθ2……(1)
スネルの法則により
n1・sinθ1 = n2・sinθ2
sinθ2=(n\(\frac{1}{n}\)2)・sinθ1
(1)に代入して、
E'=(n\(\frac{1}{n}\)2)・sinθ1- Ncosθ2……(2)
sinθ1 = | E + Ncosθ1 | より、
絶対値記号がとれて、
sinθ1 = E + Ncosθ1
(2)に代入して、
E'=(n\(\frac{1}{n}\)2)・(E + Ncosθ1)- Ncosθ2……(3)
cos2θ2=1-sin2θ2
スネルの法則により
sinθ2=(n\(\frac{1}{n}\)2)・sinθ1を代入して、
cos2θ2=1-(n\(\frac{1}{n}\)2)2・sin2θ1
平方根を取って、
cosθ2=\(\sqrt{\quad}\)(1-(n\(\frac{1}{n}\)2)2・sin2θ1)
(3)に代入して、
E'=(n\(\frac{1}{n}\)2)・(E+Ncosθ1)-N\(\sqrt{\quad}\){1-(n\(\frac{1}{n}\)2)2・sin2θ1}
=(n\(\frac{1}{n}\)2)・(E+Ncosθ1)-N(n\(\frac{1}{n}\)2)\(\sqrt{\quad}\){(n\(\frac{2}{n}\)1)2-sin2θ1}
=(n\(\frac{1}{n}\)2)・(E-N(\(\sqrt{\quad}\){(n\(\frac{2}{n}\)1)2-sin2θ1}-cosθ1))
sin2θ1=1-cos2θ1と置き換えて、
E'=(n\(\frac{1}{n}\)2)・(E-N(\(\sqrt{\quad}\){(n\(\frac{2}{n}\)1)2-1+cos2θ1}-cosθ1))
(3)より
E'=(n\(\frac{1}{n}\)2)・{E + Ncosθ1-(n\(\frac{2}{n}\)1)Ncosθ2}
=(n\(\frac{1}{n}\)2)・{E -N((n\(\frac{2}{n}\)1)cosθ2-cosθ1)}
(n\(\frac{2}{n}\)1)=nとおくと、
E'=(n\(\frac{1}{n}\)2)・{E -N(n・cosθ2-cosθ1)}
以上の変形ができます。
ウィレブロルド・スネル(オランダ、1581~1626)が光の屈折現象の
観察から見つけた屈折の法則は有名な法則ですね。
n1・sinθ1 = n2・sinθ2