質問＜２３２＞２０００／２／２４
ハサミ男という小説の中で 二子山部屋に貴乃花と若乃花、東関部屋に曙がいて、この３ 力士は彼等以外の力士に必ず勝ち、互いに対戦したときの勝 率は五分五分だとすると、貴乃花あるいは若乃花が優勝する 確率はそれぞれ８分の３で、曙が優勝する確率は４分の１で ある。 では、二子山部屋にｍ人の力士がおり、佐渡ヶ獄部屋にｎ人 の力士がいてｍはｎより大きいとする。これらの力士は他の 部屋の力士には必ず勝ち、互いに対戦した時の勝率は５分５ 分とする。このとき、それぞれの部屋から優勝力士が出る確 立を求めよ。 という問題があったんですが、まったくもって分かりません。 気になって夜も眠れないのでご存知でしたら教えて下さい。
お返事２０００／２／２６
from=武田
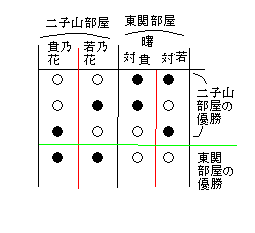
二子山部屋の貴乃花と若乃花、そして東関部屋の曙の例で 考えてみると、次のようになる。曙が優勝するのは、２人に勝ったときだから、 １ １ １ ─×─＝─ ……東関部屋が優勝する確率 ２ ２ ４ 二子山部屋が優勝する確率は、 １ ３ １－─＝─ ４ ４ 貴乃花、若乃花それぞれの優勝確率は２で割って、 ３ ３ ─÷２＝─ ４ ８ さて、質問のことですが、 二子山部屋にｍ人の力士と、佐渡ヶ獄部屋にｎ人の力士がい て、ｍはｎより大きいとする場合を考えるわけだが、 普通、変数ｍ，ｎがでてくるときは、数列的に変化させて様 子を見るのが得策なので、それでやってみましょう。 ｍ＝３、ｎ＝１の場合
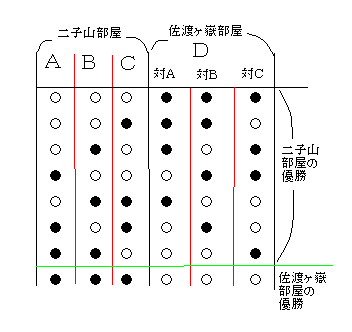
Ｄが全勝するのは、３人に勝ったときだから、 １ １ １ １ ─×─×─＝─ ……佐渡ヶ嶽部屋が優勝する確率 ２ ２ ２ ８ 二子山部屋が優勝する確率は、 １ ７ １－─＝─ ８ ８ ｍ＝３、ｎ＝２の場合 Ｄ、Ｅそれぞれが全勝するのは、３人に勝ったときだから、 １ １ １ １ ─×─×─＝─ ２ ２ ２ ８ Ｄ、Ｅ両方とも全勝するのは、 １ １ １ ─×─＝── ８ ８ ６４ 佐渡ヶ嶽部屋が優勝するのは、Ｄ∪Ｅの確率だから、 Ｐ（Ｄ∪Ｅ）＝Ｐ（Ｄ）＋Ｐ（Ｅ）－Ｐ（Ｄ∩Ｅ） １ １ １ １５ ＝─＋─－──＝── ８ ８ ６４ ６４ 二子山部屋が優勝する確率は、 １５ ４９ １－───＝── ６４ ６４ ｍ＝４、ｎ＝１の場合 Ｅが全勝するのは、４人に勝ったときだから、 １ １ １ １ １ ─×─×─×─＝── ……佐渡ヶ嶽部屋が優勝する確率 ２ ２ ２ ２ １６ 二子山部屋が優勝する確率は、 １ １５ １－──＝── １６ １６ ｍ＝４、ｎ＝２の場合 Ｅ、Ｆそれぞれが全勝するのは、４人に勝ったときだから、１ １ １ １ １ ─×─×─×─＝── ２ ２ ２ ２ １６ Ｅ、Ｆ両方とも全勝するのは、 １ １ １ ──×──＝─── １６ １６ ２５６ 佐渡ヶ嶽部屋が優勝するのは、Ｅ∪Ｆの確率だから、 Ｐ（Ｅ∪Ｆ）＝Ｐ（Ｅ）＋Ｐ（Ｆ）－Ｐ（Ｅ∩Ｆ） １ １ １ ３１ ＝──＋──－───＝─── １６ １６ ２５６ ２５６ 二子山部屋が優勝する確率は、 ３１ ２２５ １－───＝─── ２５６ ２５６ ｍ＝４、ｎ＝３の場合 Ｅ、Ｆ、Ｇそれぞれが全勝するのは、４人に勝ったときだから、 １ １ １ １ １ ─×─×─×─＝── ２ ２ ２ ２ １６ Ｅ、Ｆ、Ｇ３人とも全勝するのは、 １ １ １ １ ──×──×──＝──── １６ １６ １６ ４０９６ Ｅ∩Ｆ、Ｆ∩Ｇ、Ｅ∩Ｇの確率はそれぞれ １ １ １ ──×──＝─── １６ １６ ２５６ 佐渡ヶ嶽部屋が優勝するのは、Ｅ∪Ｆ∪Ｇの確率だから、 Ｐ（Ｅ∪Ｆ∪Ｇ） ＝Ｐ（Ｅ）＋Ｐ（Ｆ）＋Ｐ（Ｇ） －Ｐ（Ｅ∩Ｆ）－Ｐ（Ｆ∩Ｇ）－Ｐ（Ｅ∩Ｇ） ＋Ｐ（Ｅ∩Ｆ∩Ｇ） １ １ １ ７２１ ＝──×３－───×３＋────＝──── １６ ２５６ ４０９６ ４０９６ 二子山部屋が優勝する確率は、 ７２１ ３３７５ １－────＝──── ４０９６ ４０９６ ｎ＝１のときの二子山部屋の優勝確率を数列で考えて、 (２)(３)(４)……(ｍ) ３ ７ １５ ２m－１ ─、─、──……──── ４ ８ １６ ２m ｍ＝４のとき、ｎを変化させて、 (１) (２) (３)…………(ｎ) １５ ２２５ ３３７５ ２4－１ ──、───、────……（────）n １６ ２５６ ４０９６ ２4 したがって、 ｍ人いる二子山部屋Ｐとｎ人いる佐渡ヶ嶽部屋Ｑの優勝する 確率は ２m－１ Ｐ＝（────）n ……（答） ２m Ｑ＝１－Ｐ ただし、同部屋対戦はないことと、他部屋は必ず対戦するので、 １≦ｎ＜ｍ≦１５ （追伸）「全勝しないでも優勝できるかも」と言う質問があ りましたが、同点決勝となったうえでの話なので、上の解答 にもう一つ条件を付けます。 条件「同点決勝での優勝は除く」
お返事２０００／９／１５
from=武田
上の条件の「同点決勝での優勝は除く」は止めました。そのかわり、
同点決勝のときは、その人数の割合で優勝する確率を設定しました。
例えば、Ａ部屋の３人とＢ部屋の１人が、１４勝１敗で同点決勝になっ
たとすると、Ａ：Ｂ＝０．７５：０．２５として、カウントします。
計算による確率の式化はできませんでしたが、コンピュータによる計算プ
ログラムは完成しました。
２進法を利用したプログラムなので、秋の関数協の研究大会に発表するつ
もりです。
なお、このもとになるＢＡＳＩＣは、文教大学教育学部の白石和夫さんが
作った「（仮称）十進ＢＡＳＩＣ」です。昔のＢＡＳＩＣと似ているので
便利に使っています。
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
dim G(15,15),B(210),a_victor(15),b_victor(15)
!入力設定
DO
clear
print "相撲の確率 by T.Takeda"
input PROMPT "Ａ部屋の関取の数 ｍ＝":m
input PROMPT "Ｂ部屋の関取の数 ｎ＝":n
if m>n and m<=15 and n>=1 then
EXIT DO
END IF
print "入力は、１≦ｎ＜ｍ≦１５の範囲にしてください！"
LOOP
!全体初期化
LET l=n*m
LET a_count=0
LET b_count=0
LET pattern=0
DO
!内部初期化
for saisyo1=1 to l
LET B(saisyo1)=0
next saisyo1
for saisyo2=1 to m
LET a_victor(saisyo2)=0
next saisyo2
for saisyo3=1 to n
LET b_victor(saisyo3)=0
next saisyo3
LET a_max=0
LET b_max=0
!２進法化
LET keisan=pattern
for henkan=1 to l
if keisan/2<=0 then
LET B(henkan)=0
EXIT FOR
ELSEIF keisan/2<1 then
LET B(henkan)=1
EXIT FOR
ELSE
LET B(henkan)=MOD( keisan , 2 )
LET keisan=int(keisan/2)
END IF
next henkan
print pattern;"→";
for hyouji=1 to l
print B(hyouji);
next hyouji
print
!行列化
for gyou=1 to n
for retu=1 to m
LET G(gyou,retu)=B((gyou-1)*m+retu)
print G(gyou,retu);
next retu
print
next gyou
print
print
!Ａ部屋の勝敗
for rool=1 to m
for qool=1 to n
LET a_victor(rool)=a_victor(rool)+G(qool,rool)
next qool
LET a_victor(rool)=15-a_victor(rool)
print a_victor(rool);
next rool
print
print
!Ｂ部屋の勝敗
for qeel=1 to n
for reel=1 to m
LET b_victor(qeel)=b_victor(qeel)+G(qeel,reel)
next reel
LET b_victor(qeel)=15-m+b_victor(qeel)
print b_victor(qeel);
next qeel
print
print
!最大値
for raal=1 to m
LET a_max=max(a_max,a_victor(raal))
next raal
for qaal=1 to n
LET b_max=max(b_max,b_victor(qaal))
next qaal
print a_max;"勝 対 ";b_max;"勝"
print
!カウント
if a_max>b_max then
LET a_count=a_count+1
ELSEIF a_max<b_max then
LET b_count=b_count+1
ELSE
LET s_count=0
LET t_count=0
LET goukei=0
for s=1 to m
if a_max=a_victor(s) THEN
LET s_count=s_count+1
end if
next s
for t=1 to n
if b_max=b_victor(t) THEN
LET t_count=t_count+1
end if
next t
LET goukei=s_count+t_count
LET c=round(s_count/goukei,5)
LET d=round(t_count/goukei,5)
print c;d
LET a_count=a_count+c
LET b_count=b_count+d
END IF
print ;"Ａ部屋";a_count;"Ｂ部屋";b_count
print
!繰り返し条件
LET pattern=pattern+1
IF pattern>=2^l then
EXIT DO
END IF
loop
!最後の表示
print
print "Ａ部屋(";m;"人)優勝の確率";round(a_count/(2^l),5)*100;"％"
print "Ｂ部屋(";n;"人)優勝の確率";round(b_count/(2^l),5)*100;"％"
end
＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊
なお、結果ですが、時間がかかるので、以下の例しかやっていません。
Ａ部屋( 2 人)優勝の確率 75 ％：Ｂ部屋( 1 人)優勝の確率 25 ％
Ａ部屋( 3 人)優勝の確率 87.5 ％：Ｂ部屋( 1 人)優勝の確率 12.5 ％
Ａ部屋( 3 人)優勝の確率 69.531 ％：Ｂ部屋( 2 人)優勝の確率 30.469 ％
Ａ部屋( 4 人)優勝の確率 93.75 ％：Ｂ部屋( 1 人)優勝の確率 6.25 ％
Ａ部屋( 4 人)優勝の確率 82.578 ％：Ｂ部屋( 2 人)優勝の確率 17.422 ％
Ａ部屋( 4 人)優勝の確率 67.144 ％：Ｂ部屋( 3 人)優勝の確率 32.856 ％