いま学校で積分演習をやっているのですがいまいちよくわかりません。
三問ほどですがおねがいします
一問目
数列{Cn}を次の式で定める。
Cn=(n+1)∫0から1 (\(x^{n}\)・cosπx・dx)(n=1,2,,,,)
このとき次の問いに答えよ
(1)CnとCn+2 の関係を求めよ
(2)Lim n→∞ Cn を求めよ
(3) (2)で求めた極大値をcとするとき
Lim n→∞ (Cn+1-C/Cn-C)を求めよ
二問め
nは自然数とし、An=(1+\(\frac{1}{2}\)+\(\frac{1}{3}\)+、、、+\(\frac{1}{n}\))-logn
とおく。y=\(\frac{1}{x}\)(x>0)のグラフと∫\(\frac{1}{x}\)・dx を考えることにより、数列
A1,A2,A3,,,,,,,An,,,,,の性質を調べる
(1)An>\(\frac{1}{n}\)(n≧2)を示せ
(2)An>An+1 を示せ
(3) y=\(\frac{1}{x}\) (x>0) のグラフが下に凸であることを用いて
\(\frac{1}{2}\)(\(\frac{1}{n}\) + \(\frac{1}{n}\)+1)>log(n+1)-logn を示せ
(4) An>(\(\frac{1}{2}\) + \(\frac{1}{2}\)n) (n≧2)を示せ
最終問題
次を示せ
(1)log(n+1)<1 + \(\frac{1}{2}\) + \(\frac{1}{3}\) 、、、+\(\frac{1}{n}\) (n=1,2,3,,)
(2)Lim n→∞ {\(\frac{1}{l}\)ogn ・Σ k=1~n (1/K)}=1
(3)Lim n→∞ {\(\frac{1}{l}\)ogn・∫1~n+1(|sinπ\(\frac{x}{x}\)|dx)}
=∫0~1 (sinπy・dy)=2/π
問1
(1)
Cn =(n+1)∫0 1 (xn cosπx)dx
xn+1 xn+1
=(n+1){[───cosπx]0 1 -∫0 1 ───(-πsinπx)dx}
n+1 n+1
1 π
=(n+1){-───-0+───∫0 1 (xn+1 sinπx)dx}
n+1 n+1
xn+2 xn+2
=-1+π{[───sinπx]0 1 -∫0 1 ───(πcosπx)dx}
n+2 n+2
π
=-1+π{0-0-───∫0 1 (xn+2 cosπx)dx}
n+2
π2 n+3
=-1-───・───∫0 1 (xn+2 cosπx)dx}
n+2 n+3
π2
=-1-─────・Cn+2 ……(答)
(n+2)(n+3)
(2)
π2
Cn =-1-─────・Cn+2
(n+2)(n+3)
π2 π2
=-1-─────{-1-──────・Cn+4 }
(n+2)(n+3) (n+4)(n+5)
π2 π4 π2
=-1+─────+───────────{-1-─────・Cn+6 }
(n+2)(n+3) (n+2)(n+3)(n+4)(n+5) (n+6)(n+7)
π2 π4
=-1+─────-───────────-……
(n+2)(n+3) (n+2)(n+3)(n+4)(n+5)
lim Cn =-1 ……(答)
n→∞
π2
(3) -1-──────・Cn+3 -(-1)
Cn+1 -c (n+3)(n+4)
lim ────────=lim ────────────────
n→∞ Cn -c n→∞ π2
-1-─────・Cn+2 -(-1)
(n+2)(n+3)
(n+2)Cn+3
=lim ─────────
n→∞ (n+4)Cn+2
(1+2/n)Cn+3
=lim ──────────
n→∞ (1+4/n)Cn+2
(1+0)・(-1)
=──────────=1……(答)
(1+0)・(-1)
問2(1)
nは自然数とし、An=(1+\(\frac{1}{2}\)+\(\frac{1}{3}\)+、、、+\(\frac{1}{n}\))-logn
とおく。An>\(\frac{1}{n}\)(n≧2)を示せ。
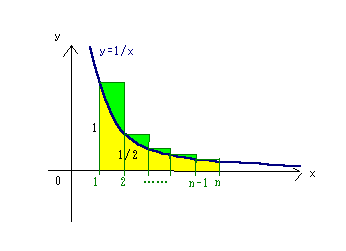
図より、長方形の面積の和は黄色の積分の面積より大きいので、
n-1 1 n 1
Σ (──×1)>∫ ───dx
k=1 k 1 x
1 1 1 n
1+─+─+……+──>[log|x|]
2 3 n-1 1
1 1 1 1 1
1+─+─+……+──+──>logn+──
2 3 n-1 n n
1
An>── ……(答)
n
問2(2)
An>An+1 を示せ。
P=An-An+1とおくと、
P={(1+……+\(\frac{1}{n}\))-log n}-{(1+……+1/(n+1))-log(n+1)}
=-1/(n+1)+log(n+1)-log n
=log{(n+1)/n}-1/(n+1)
=log(1+1/n)-(\(\frac{1}{n}\))/(1+\(\frac{1}{n}\))
\(\frac{1}{n}\)=xとおいて、関数化して、
x
f(x)=log(1+x)-───
1+x
微分して、
1 (1+x)-x
f′(x)=───-────
1+x (1+x)2
1+x-1 x
=─────=────
(1+x)2 (1+x)2
n≧1より、0<1/n≦1
0<x≦1において、
f(0)=0、f′(0<x≦1)>0より、f(x)>0
x
f(x)=log(1+x)-───>0
1+x
n+1 1
log(───)-───>0
n n+1
P>0
したがって、An-An+1>0
∴An>An+1 ……(答)
問2(3)
y=\(\frac{1}{x}\) (x>0) のグラフが下に凸であることを用いて
\(\frac{1}{2}\)(\(\frac{1}{n}\) + \(\frac{1}{n}\)+1)>log(n+1)-logn を示せ。
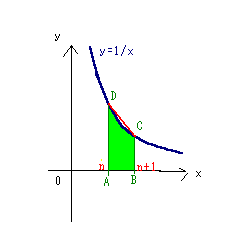
台形ABCDの面積は積分の面積より大きいから、
台形の面積=(上底+下底)×高さ÷2より、
1 1 n+1 1
(─+───)×1÷2>∫ ──dx
n n+1 n x
したがって、
1 1 1
─(─+───)>log(n+1)-logn ……(答)
2 n n+1
問2(4)
An>(\(\frac{1}{2}\) + \(\frac{1}{2}\)n) (n≧2)を示せ。
前の式にn=1から順に代入し、総和を求めると、
1 1 1
n=1 ─(─+─)>log2-log1
2 1 2
1 1 1
n=2 ─(─+─)>log3-log2
2 2 3
1 1 1
n=3 ─(─+─)>log4-log3
2 3 4
……
1 1 1
n=n-1 ─(───+─)>logn-log(n-1)
2 n-1 n (+
──────────────────────────────
1 1 1 1 1 1 1
─(1+─+─+……+───+─+─+……+─)>logn-log1
2 2 3 n-1 2 3 n
1 1 1 1 1
─{2(1+─+─+……+─)-1-─}>logn
2 2 3 n n
1 1 1 1 1
(1+─+─+……+─)-logn>─(1+─)
2 3 n 2 n
1 1
∴An>──+─── ……(答)
2 2n
問3(1)
log(n+1)<1 + \(\frac{1}{2}\) + \(\frac{1}{3}\) 、、、+\(\frac{1}{n}\) (n=1,2,3,,)を示せ。
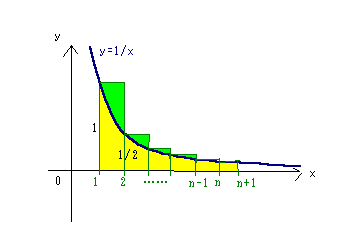
長方形の1からn+1までの面積の和は積分の面積より大きいから、
n 1 n+1 1
Σ ── >∫ ───dx
k=1 k 1 x
したがって、
1 1 1
1+─+─+……+─ > log(n+1)……(答)
2 3 n
問3(2)
Lim n→∞ {\(\frac{1}{l}\)ogn ・Σ k=1~n (1/K)}=1を示せ。
公式
1 1 1
log(n+1)<1+─+─+……+─<logn +1
2 3 n
log(n+1) 1 n 1 logn +1
────────<──── Σ ── <────────
logn logn k=1 k logn
ロピタルの定理より、
1
───
log(n+1) n+1 n
lim────────=lim───────=lim ───
n→∞ logn n→∞ 1 n→∞ n+1
────
n
1 1
=lim ─────=───=1……①
n→∞ 1+1/n 1+0
1
───
logn +1 n
lim────────=lim───────=lim 1=1……②
n→∞ logn n→∞ 1 n→∞
────
n
①と②より、挟み込み法により、
1 n 1
lim ──── Σ ── =1……(答)
n→∞ logn k=1 k
問3(3)
Lim n→∞ {\(\frac{1}{l}\)ogn・∫1~n+1(|sinπ\(\frac{x}{x}\)|dx)}
=∫0~1 (sinπy・dy)=2/πを示せ。
これだけは流石に分かりませんでした。
未解決問題のコーナーに移させてもらいましたところ、
マスマニアさんから有り難い解答を頂きました。感謝!!