問１
［確率］の方は、未解決問題の方に移しましたが、川口高志さんから
お便りをいただきました。ヒントとなる考え方がありました。やはり、
確率は発想ですね。川口さんに感謝！！下にお便りとして掲載しました。

問２（１）
［数列］
１群　１
２群　２　　４
３群　３　　６　　９
４群　４　　８　１２　１６
５群　５　１０　１５　２０　２５
６群　６　１２　１８　２４　３０　３６

ｋ群のｌ番目をａ_k,lとすると、
ａ_k,l＝ｋ＋（ｌ－１）・ｋ＝ｋｌ
自然数ｍ＝ｋｌ（ただし、ｋ≧ｌ）より、
ｍ　　１　２　３　　４　　５　　６　　……
ｋ　　１　２　３　４　２　５　６　３　……
ｌ　　１　１　１　１　２　１　１　２　……
f(m)　１　１　１　　２　　１　　２　　……

例えば１８と言う数は６群の３列目にあるが、
１８を２つの数の積に直すと、
１８＝１８×１，９×２，６×３，
　　　３×６，２×９，１×１８
１８群１列と９群２列と６群３列の３カ所に出てくる。ｋ≧ｌより、
下の３カ所は存在しない。
したがって、ｆ（１８）＝３となる。

同様に２４を例にとると、
２４＝２４×１，１２×２，８×３，６×４，
　　　４×６，３×８，２×１２，１×２４
２４群１列と１２群２列と８群３列と６群４列の４カ所に出てくる。
同様に下の４カ所は存在しない。
したがって、ｆ（２４）＝４

同様に３６を例にとると、
３６＝３６×１，１８×２，１２×３，９×４，６×６，
　　　４×９，３×１２，２×１８，１×３６
したがって、ｆ（３６）＝５

以上の３例から、ｆ（ｍ）の式を作るために、素因数分解を利用する。
１８＝２×３×３＝２×３²
約数の個数は（１＋１）×（２＋１）＝２×３＝６
半分は使わないので、６÷２＝３
したがって、ｆ（１８）＝３
２４＝２×２×２×３＝２³ ×３
約数の個数は（３＋１）×（１＋１）＝４×２＝８
半分は使わないので、８÷２＝４
したがって、ｆ（２４）＝４
３６＝２×２×３×３＝２² ×３²
約数の個数は（２＋１）×（２＋１）＝３×３＝９
９÷２＝４．５　四捨五入して、５
これは６×６を繰り入れているからこうなる。
したがって、ｆ（３６）＝５

以上より、ｆ（ｍ）＝５となるのは、５と４．５のときだから、
２倍して、約数の個数が１０個、または９個のときである。
１０個＝１０×１，５×２，２×５，１×１０
指数で考えると、９乗単独、４乗×１乗を探すと、
２⁹ ＝５１２
３⁹ ＝１９６８３
……
２⁴ ×３＝１６×３＝４８
２⁴ ×５＝１６×５＝８０
２⁴ ×７＝１６×７＝１１２
２⁴ ×１１＝１６×１１＝１７６
２⁴ ×１３＝１６×１３＝２０８
……
３⁴ ×２＝８１×２＝１６２
３⁴ ×５＝８１×５＝４０５
……
５⁴ ×２＝６２５×２＝１２５０
……
次に、９個＝９×１，３×３，１×９
指数で考えると、８乗単独、２乗×２乗を探すと、
２⁸ ＝２５６
３⁸ ＝６５６１
……
２² ×３² ＝４×９＝３６
２² ×５² ＝４×２５＝１００
２² ×７² ＝４×４９＝１９６
２² ×１１² ＝４×１２１＝４８４……
３² ×５² ＝９×２５＝２２５
……
これらの数がｆ（ｍ）＝５となるわけだから、小さい方から並べると、
３６，４８，８０，１００，１１２、１６２，１７６，１９６，……（答）

Ｂａｓｉｃのプログラムを作って確かめてみると、
##############################################################
100 '素因数分解を利用したfm=5を求めるプログラム
110 dim s(1000)
120 cls
130 for t=2 to 1000
140 for j=2 to t:s(j)=0:next j
150 j=2:s(0)=1:fm=0:i=t
160 if j＞sqr(i+1) goto 200
170 if i-int(\(\frac{i}{j}\))*j=0 then s(j)=s(j)+1:goto 190
180 j=j+1:goto 160
190 i=\(\frac{i}{j}\):goto 160
200 s(i)=s(i)+1
210 for j=2 to t
220 if s(j)＜＞0 then s(0)=s(0)*(s(j)+1)　　’ここがポイント
230 next j
240 if s(0)/2-int(s(0)/2)＞0 then fm=int(s(0)/2)+1:goto 260
250 fm=s(0)/2
260 if fm=5 then print t;
270 next t
280 end
##############################################################
すると、ｆ（ｍ）＝５となる自然数ｍの列
３６，４８，８０，１００，１１２，１６２，１７６，……
とでてきます。

問（２）
例えば、２４で考えると、
２４＝２³ ×３より、
約数の個数は、（３＋１）×（１＋１）＝４×２＝８
８÷２＝４　したがって、ｆ（２４）＝４
２４の２倍は４８だから、
４８＝２×２４＝２×２³ ×３＝２⁴ ×３
約数の個数は（４＋１）×（１＋１）＝５×２＝１０
１０÷２＝５　したがって、ｆ（４８）＝５
２×ｆ（２４）≠ｆ（２・２４）

例えば、１５＝３×５
約数の個数は２×２＝４
４÷２＝２　したがって、ｆ（１５）＝２
１５の２倍は、３０＝２×３×５
約数の個数は２×２×２＝８
８÷２＝４　したがって、ｆ（３０）＝４
２×ｆ（１５）＝ｆ（２・１５）

例えば、奇数の平方数２５＝５²
約数の個数は３
３÷２＝１．５つまり２　したがって、ｆ（２５）＝２
２５の２倍は、５０＝２×５²
約数の個数は２×３＝６
６÷２＝３　したがって、ｆ（５０）＝３
２×ｆ（２５）≠ｆ（２・２５）

例えば、２のとき、
約数の個数は２
２÷２＝１　したがって、ｆ（２）＝１
２の２倍は、４＝２²
約数の個数は３
３÷２＝１．５　つまり２　したがって、ｆ（４）＝２
２×ｆ（２）＝ｆ（２・２）

例えば、１のとき、
約数の個数は１
１÷２＝０．５　つまり１　したがって、ｆ（１）＝１
１の２倍は、２
約数の個数は２
２÷２＝１　したがって、ｆ（２）＝１
２×ｆ（１）≠ｆ（２・１）

以上から、２×ｆ（ｍ）＝ｆ（２・ｍ）が成り立つのを小さい方
から並べると、
２，３，５，７，１１，１３，１５，１７，１９，２１，２３，２７，……（答）

これもパソコンで確認すると、
##############################################################
100 '素因数分解を利用した２×ｆ（ｍ）＝ｆ（２・ｍ）となるｍを
　　　求めるプログラム
110 dim s(1000),f(1000)
120 cls
130 for u=2 to 200:f(u)=0:next u
140 for p=2 to 200
150 for q=2 to p:s(q)=0:next q
160 j=2:s(0)=1:i=p
170 if j>sqr(i+1) goto 210
180 if i-int(\(\frac{i}{j}\))*j=0 then s(j)=s(j)+1:goto 200
190 j=j+1:goto 170
200 i=\(\frac{i}{j}\):goto 170
210 s(i)=s(i)+1
220 for r=2 to p
230 if s(r)<>0 then s(0)=s(0)*(s(r)+1)
240 next r
250 if s(0)/2-int(s(0)/2)>0 then f(p)=int(s(0)/2)+1:goto 270
260 f(p)=s(0)/2
270 next p
280 for t=2 to 100:a=2*f(t):b=f(2*t)
290 if a=b then print t;:goto 300
295 print "*";
300 next t
310 end
##############################################################
２，３，５，７，１１，１３，１５，１７，１９，２１，２３，２７，……
これを自然数１００まで調べてみると、
２と、３以降の奇数の列（平方数は除く）と言うことが確認できた。

問１
こんにちは。

未解決問題の確率なのですがこれってそんなに難しい問題なのでしょうか?

>[確率]
>M姉妹、T姉妹、N姉妹、G姉妹の計8名が
>円形のテーブルの周りに無作為にすわるとき
>姉妹同士が一組も隣り合わない確率を求めよ

［解］
2組の姉妹の座り方x2は2通り．
3組の場合x3は，x2の間のどこかに，2人入ることになるので，
x3=x2+4P2=2+12=14
4組のときは，6つの間のどこかに2人はいるので，
x4=x3+6P2=14+30=44
求める確率は
p(4)=\(\frac{44}{7}\)!=\(\frac{11}{420}\)

これで大丈夫だと思うのですが考え違いがありますでしょうか・・・

問１
>[確率]
>M姉妹、T姉妹、N姉妹、G姉妹の計8名が
>円形のテーブルの周りに無作為にすわるとき
>姉妹同士が一組も隣り合わない確率を求めよ

［正解］
2組の姉妹の座り方をまず考える。
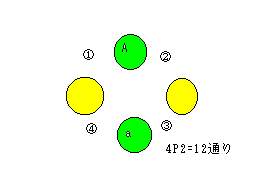
ある姉妹の姉Ａを固定すると、その反対側に妹ａ
すると、もう一組の姉妹は黄色２カ所に入れれば、隣接しないから
₂ Ｐ₂ ＝２！＝２通り。


姉妹３組の場合は、上の図の間の４カ所に残りの姉妹が入れば、隣接
しないから、₄ Ｐ₂ ＝１２通り

積の法則より、
２×１２=２４通り

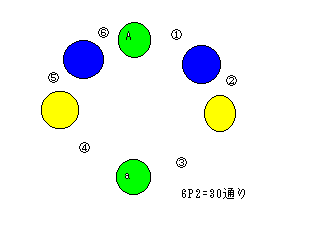
姉妹４組の場合は、上の図の２カ所に三番目の姉妹が入ったとして、
青色で表すと、残りの姉妹は間の６カ所の中から２カ所選べば、隣接
しないから、₆ Ｐ₂ ＝３０通り

したがって、積の法則より
２４×３０＝７２０通り

求める確率は
　　　　　　　７２０　　　７２０　　１
Ｐ（４）＝──────＝─────＝─　……（答）
　　　　　（８－１）！　５０４０　　７