質問

問１
三角形ABCの3頂点A,B,Cから対辺にひいた垂線の長さが、
それぞれ、4.3.6のとき，次の問いに答えよ。
①　3辺の比a:b:cを求めよ。
②　最小頂角の余弦を求めよ。
③　3辺a,b,cの長さを求めよ

問２
半径が1の円に内接する正八角形の面積を求めよ

問３
一辺の長さがaである正四面体の体積を求めよ。また、この正四面体に
外接する球の半径を求めよ。

問４
水平におかれた平面の板に3辺の長さ13.14.15の三角形の穴があいている。
この穴に半径5の球に乗せたとき、板の上面から球の対抗店までの高さを
求めよ。

問５
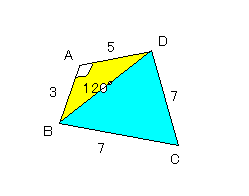
AB=3,BC=7,CD=7,DA=5,A=120゜である四角形ABCDについて、
次のものを求めよ。
①　対角線BDの長さ
②　四角形ABCDの面積S

問６
四角形の二つの対下線のa,b,cその交角をθとするとき、
この四角形の面積は、1/2absinθで与えられることを証明せよ。

お返事２０００／８／２３
from=武田

問１
①

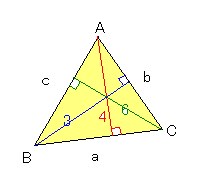
正弦定理より
sinＡ＝６／ｂ、sinＡ＝３／ｃより、６／ｂ＝３／ｃ
ｂ：ｃ＝６：３＝２：１＝４：２
sinＢ＝４／ｃ、sinＢ＝６／ａより、４／ｃ＝６／ａ
ａ：ｃ＝６：４＝３：２
したがって、ａ：ｂ：ｃ＝３：４：２……（答）

②

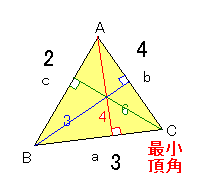
比の中の最小の辺ｃの対頂角Ｃの余弦は、余弦定理より、
角度なので、辺の比の状態でも求まる。
　　　　ａ²＋ｂ²－ｃ²　　３²＋４²－２²　９＋１６－４
cosＣ＝────────＝────────＝───────
　　　　　　２ａｂ　　　　　２・３・４　　　　　２４

　　　２１　７
　　＝──＝─　……（答）
　　　２４　８

③
　　　　　　　　　　　　　４９　１５
sin²Ｃ＝１－cos²Ｃ＝１－──＝──
　　　　　　　　　　　　　６４　６４
∠Ｃは最小なので鋭角となるから、sinＣ＞０より、
　　　　√１５
sinＣ＝────
　　　　　８
sinＣ＝３／ａより、

　　　　　３　　　　２４　２４√１５　８√１５
ａ＝──────＝───＝─────＝────　……（答）
　　　√１５　　　√１５　　１５　　　　　５
　　　────
　　　　　８
ａ：ｂ：ｃ＝３：４：２より、

　　４　　　４　８√１５　３２√１５
ｂ＝─・ａ＝─・────＝─────　……（答）
　　３　　　３　　　５　　　１５

　　２　　　２　８√１５　１６√１５
ｃ＝─・ａ＝─・────＝─────　……（答）
　　３　　　３　　　５　　　１５

問２

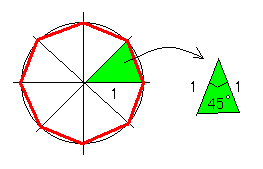
正８角形の１つの三角形の内角は、３６０°÷８＝４５°
三角形の面積の公式より、
Ｓ＝（１／２）・１・１・sin４５°
　＝（√２）／４
正８角形の面積は８倍して、
８Ｓ＝２√２　……（答）

問３

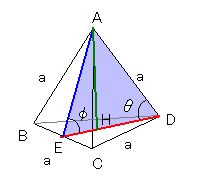
△ＣＤＥにおいて、ＤＥ＝ａsin６０°＝（√３ａ）／２
垂心Ｈは△ＢＣＤの重心だから、ＤＥを２：１に内分する。
　　　　　　２　√３ａ　２　√３
ＤＨ＝ＤＥ・─＝───・─＝──ａ
　　　　　　３　　２　　３　　３
△ＡＤＨより、
　　　　　　　　√３
　　　　　　　　──ａ
　　　　ＤＨ　　　３　　　√３
cosθ＝───＝────＝───
　　　　ＡＤ　　　ａ　　　　３
図より、sinθ＞０
　　　　　　　　　　　　　３　６　２
sin²θ＝１－cos²θ＝１－─＝─＝─
　　　　　　　　　　　　　９　９　３
　　　　√２　　√６
sinθ＝───＝───
　　　　√３　　　３
したがって、
　　　　　　　　　　√６
ＡＨ＝ａsinθ＝ａ・───
　　　　　　　　　　　３
底面△ＢＣＤの面積は
　　１　　　　　　　１　　　√３　　√３
Ｓ＝─・ＢＣ・ＤＥ＝─・ａ・──ａ＝──ａ²
　　２　　　　　　　２　　　　２　　　４
１辺ａの四面体の体積は
　　１　　　　　　１　√６　　√３
Ｖ＝─・ＡＨ・Ｓ＝─・──ａ・──ａ²
　　３　　　　　　３　　３　　　４

　　√１８　　　３√２　　　√２
　＝───ａ³＝───ａ³＝──ａ³　……（答）
　　　３６　　　　３６　　　１２

この正四面体に外接する球の半径をｒとすると、

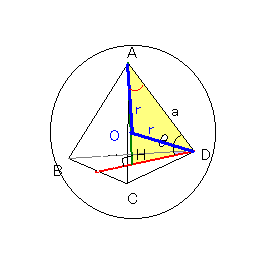
△ＡＤＨにおいて、
∠ＤＡＨ＝９０°－θ
二等辺三角形△ＡＯＤより、
ａ＝２・ｒ・cos∠ＤＡＨ＝２ｒcos（９０°－θ）＝２ｒsinθ

　　　　　√６
　＝２ｒ・──
　　　　　　３
したがって、
　　　　　３　　３√６　　√６
ｒ＝ａ・───＝───ａ＝──ａ　……（答）
　　　　２√６　　１２　　　４

問４
文章の中に誤字がありましたが、「対抗店」とは「最高点」でしょうか？

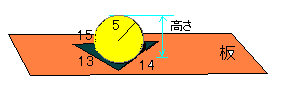
板の中に開けた三角形の３辺１３，１４，１５の中にはまる内接円の半径
ｒを求めてみると、

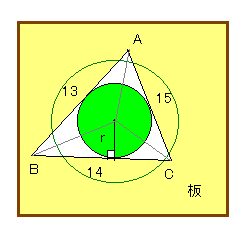
ヘロンの公式より、２ｓ＝１３＋１４＋１５＝４２
ｓ＝２１
Ｓ＝√｛２１・（２１－１３）（２１－１４）（２１－１５）｝
　＝√（２１・８・７・６）＝√７０５６＝８４
また、３つの三角形の面積の和より、
Ｓ＝（１／２）・１４ｒ＋（１／２）・１５ｒ＋（１／２）・１３ｒ
　＝（ｒ／２）・（１４＋１５＋１３）
　＝（ｒ／２）・４２＝２１ｒ
したがって、
８４＝２１ｒ
∴ｒ＝４
半径５の球ははまるだけで、下に落ちないから

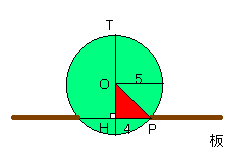
この図より、
ＯＰ²＝ＯＨ²＋ＰＨ²
５²＝ＯＨ²＋４²
したがって、
ＯＨ²＝９
∴ＯＨ＝３
最高点Ｔから板の水平線ＰＨまでの高さは
ＴＨ＝ＴＯ＋ＯＨ
　　＝５＋３＝８　……（答）

問５

①
△ＡＢＤにおいて、余弦定理より
ＢＤ²＝９＋２５－３０cos１２０°
　　　＝３４－３０・（－１／２）
　　　＝４９
ＢＤ＞０より、
ＢＤ＝７　……（答）

②
三角形の面積の公式より
△ＢＣＤは正三角形だから、
　　　１　　　　　　　　　　４９√３
Ｓ₁＝─・７・７sin６０°＝─────
　　　２　　　　　　　　　　　　４
△ＡＢＤより、
　　　１　　　　　　　　　　　１５√３
Ｓ₂＝─・３・５sin１２０°＝─────
　　　２　　　　　　　　　　　　４
したがって、
　　　　　　　　６４√３
Ｓ＝Ｓ₁＋Ｓ₂＝────＝１６√３　……（答）
　　　　　　　　　　４

問６

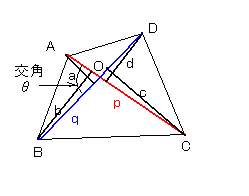
文章の誤りがあります。「対下線」でなくて「対角線」
「ａｂｃ」でなくて「ａｂ」の２つです。
今、図の都合で、２つの対角線ａ、ｂをｐ、ｑとして求めてみます。
補助線として、頂点Ａ、Ｂ、Ｃ、Ｄからそれぞれ対角線へ垂線を下ろします。
その長さをそれぞれａ、ｂ、ｃ、ｄとします。
コセカントを利用して、
ＯＡ＝ａcosecθ、ＯＣ＝ｃcosecθより、
ＡＣ＝ＯＡ＋ＯＣ＝（ａ＋ｃ）cosecθ
ｐ＝（ａ＋ｃ）cosecθ
同様にして
ＯＢ＝ｂcosecθ、ＯＤ＝ｄcosecθより、
ＢＤ＝ＯＢ＋ＯＤ＝（ｂ＋ｄ）cosecθ
ｑ＝（ｂ＋ｄ）cosecθ

この２式を掛けて、
ｐｑ＝（ａ＋ｃ）（ｂ＋ｄ）cosec²θ
したがって、（ａ＋ｃ）（ｂ＋ｄ）＝ｐｑ・sin²θ

四辺形の面積Ｓは、
Ｓ＝（１／２）ｐｂ＋（１／２）ｐｄ＝（１／２）ｐ（ｂ＋ｄ）
一方、
Ｓ＝（１／２）ｑａ＋（１／２）ｑｃ＝（１／２）ｑ（ａ＋ｃ）

この２式を掛けて、
　　　１　　　　　　　１　　　　　　　１
Ｓ²＝─ｐ（ｂ＋ｄ）・─ｑ（ａ＋ｃ）＝─ｐｑ（ａ＋ｃ）（ｂ＋ｄ）
　　　２　　　　　　　２　　　　　　　４

　　　１
　　＝─ｐｑ・ｐｑ・sin²θ
　　　４
平方根をとって、
　　１
Ｓ＝─ｐｑsinθ　……（答）
　　２