問1
a≠b≠c≠a,\(a^{3}\)+2a=\(b^{3}\)+2b=\(c^{3}\)+2cのとき
a+b+c=0,ab+bc+ca=2であることを証明せよ。
問2
p,qは、p+q=1(0≦p≦1)をみたしている。
関数f(x)=x^2について、次の不等式が成り立つことを証明せよ。
f(px+qy)≦p・f(x)+q・f(y)
おねがいします。
問1
x3 +2x=0の3解をa,b,c(a≠b≠c)とすると、
(x-a)(x-b)(x-c)=0
x3 -(a+b+c)x2 +(ab+bc+ca)x-abc=0
係数を比べて、
a+b+c=0、ab+bc+ca=2 ……(答)
問2
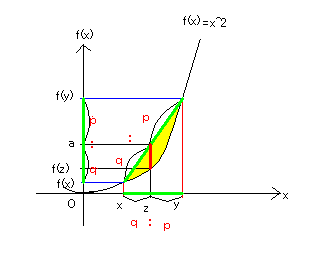
z=px+qyとおくと、p+q=1(0≦p≦1)より、
px+qy
z=───── と書ける。
q+p
したがって、xy間をq:pに内分する点にzがある。
これは、関数f(x)=x2 より、f(z)=f(px+qy)となる。
比例関係より、f(x)とf(y)間もq:pに内分する点ができる。
これをaとすると、
p・f(x)+q・f(y)
a=─────────────=p・f(x)+q・f(y)
q+p
関数f(x)=x2 は下に凸なので、図より
a≧f(z)
となる。(等号はp=0または1のとき)
したがって、
f(px+qy)≦p・f(x)+q・f(y) ……(答)