再考して何とか出来た。

１　　ａ² ＋ｂ² ＋ｃ² 　２
―≦─────────＜─
２　　　（ｃ－ａ）² 　　３

中辺をＡとおく。１／２≦Ａ＜２／３となることを導く。
ａ² ＋ｂ² ＋ｃ²
───────── ＝Ａより、
　（ｃ－ａ）²

ａ² ＋ｂ² ＋ｃ² ＝Ａ（ｃ－ａ）²
ａ＋ｂ＋ｃ＝０より、ｂ＝－ａ－ｃを代入して、
（２－Ａ）ａ² ＋２（Ａ＋１）ａｃ＋（２－Ａ）ｃ² ＝０……①
実数解ａを持つためには、方程式①の判別式Ｄ≧０より、
Ｄ／４＝（Ａ＋１）² ｃ² －（２－Ａ）（２－Ａ）ｃ²
　　　＝ｃ² （Ａ² ＋２Ａ＋１－４＋４Ａ－Ａ² ）
　　　＝ｃ² （６Ａ－３）≧０
ｃ² ≧０より、６Ａ－３≧０
したがって、
　　　１
Ａ≧───……（ア）
　　　２

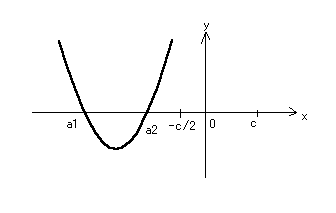
ａ＜ｂ＜ｃ、ａ＋ｂ＋ｃ＝０より、
ａ＜ｂ
ａ＜－ａ－ｃ
２ａ＜－ｃ
ａ＜－ｃ／２……②
方程式①の解の大きい方ａ２が②より左側になくてはならないので、
－（Ａ＋１）ｃ＋\(\sqrt{\quad}\)｛ｃ² （６Ａ－３）｝　　　ｃ
───────────────────＜－───
　　　　　　２－Ａ　　　　　　　　　　　　　２

－（Ａ＋１）ｃ＋ｃ\(\sqrt{\quad}\)（６Ａ－３）　　　ｃ────────────────＜－───
　　　　　　２－Ａ　　　　　　　　　　２
分母２－Ａ＞０のとき、Ａ＜２……③
－２Ａ－２＋２\(\sqrt{\quad}\)（６Ａ－３）＜－（２－Ａ）
２\(\sqrt{\quad}\)（６Ａ－３）＜－２＋Ａ＋２Ａ＋２
２\(\sqrt{\quad}\)（６Ａ－３）＜３Ａ
両辺を２乗して、
４（６Ａ－３）＜９Ａ²
９Ａ² －２４Ａ＋１２＞０
因数分解して、（３Ａ－６）（３Ａ－２）＞０
　　　２
Ａ＜───，２＜Ａ……④
　　　３
　　　　　　　　　２
③と④より、Ａ＜───……（イ）
　　　　　　　　　３
（ア）（イ）より、
１　　　２
─≦Ａ＜─……（答）
２　　　３

（追伸）
なお、分母２－Ａ＜０のときは、Ａ＞２
計算した結果は、
２
─＜Ａ＜２より、
３
共通部分はない。