質問

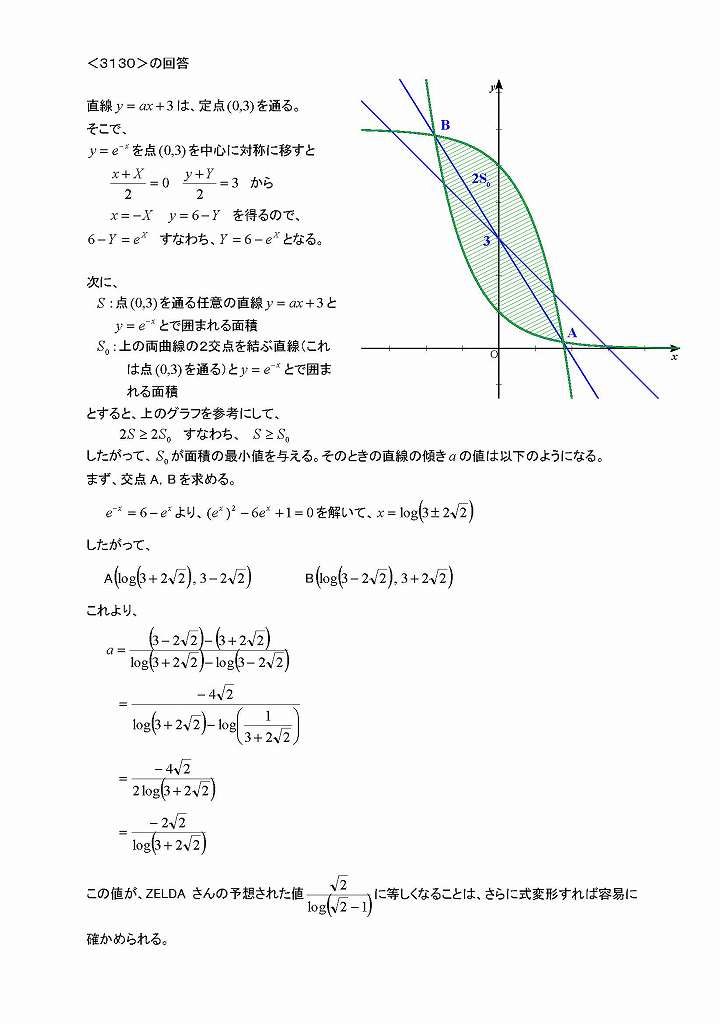
曲線y=e^(-x)と直線y=ax+3(a＜0)とが囲む図形の面積を最小にするaの値を求めよ。

曲線と直線の交点が求まらないのにどうすればよいのでしょうか？
2つの交点のx座標をs,tとおいて、これらの関係式からs,tを消去することもできそう
にありませんでした。
ただ、曲線と直線の交点をA,B(Bのほうがx座標が大きい)として、
直線とy軸との交点をCとした場合にAC=BCとなる場合に面積は最小になりそうです。
このときのaの値は,
√2/log[(√2)-1]
になります。
どなたか、御教授ください。お願いします。

★希望★完全解答★

お便り２００６／５／６
from=UnderBird

お便り２００６／９／１１
from=平　昭

こんにちは。
　すでに出ている回答は、いわゆる「はみ出し削り論法」による見事なもので、
感心しました。（０、３）を中心にして対称な曲線を持ってくる、という閃きがすごい。
私は閃かなかったので、地道にやってみました。
　ところで、今の高校生は、極座標表示による積分で面積を出す方法、というのを習って
いるのでしょうか。これを知らないと、ちょっと難しい問題かと思います。

【回答】
　直線y=ax+3(a＜0)を、y=tanθｘ＋３（π/2＜θ＜π）と表し、
この直線と曲線y=e^(-x)との交点をそれぞれ、
Ａ（ｒcosθ、ｒsinθ＋３)、
Ｂ（ｒcos（θ＋π）、ｒsin（θ＋π）＋３)
とおく。ここで、ｒはθの関数ｒ（θ）であり、ｒ＞０とする。θの範囲より、
Ａは第二象限、Ｂは第四象限の点となる。
(図を描くと分かりやすいのですが、私には
パソコン上で図が描けませんm(__)m。
これはつまり、点(０、３)を中心とした極座標表示です。)

この時、求める面積をＳ＝Ｓ（θ）とすると、
２Ｓ（θ）＝∫ｒ（φ）^2ｄφ
（積分区間がθから（θ＋π）までの定積分）と書ける、、、★

(これも図があると分かりやすいのですが、
ＡからＢまで左回りに１８０度回って積分するわけです。）

これより
２ｄＳ/ｄθ＝ｒ（θ＋π）^2－ｒ（θ）^2
　　　　 ＝{ｒ（θ＋π）－ｒ（θ）}{ｒ（θ＋π）＋ｒ（θ）}となる

　ここで、Ａ、Ｂのｙ座標を考えれば
Ａ、Ｂはy=e^(-x)上の点でもあることより、

r(θ)sinθ＋３＝e^(-ｒcosθ)　
r(θ)＝{e^(-ｒcosθ)－３ }/sinθ

ｒ（θ＋π）・sin(θ＋π)＋３＝e^(-ｒcos(θ＋π))
ｒ（θ＋π）＝{e^(ｒcosθ)－３ }/－sinθ

よって、e^(-ｒcosθ)＝Ｙとおけば

２ｄＳ/ｄθ＝－（Ｙ＋1/Y－６)(Ｙ－1/Y)/(sinθ)^2
         ＝－(Ｙ^2－６Ｙ＋１）（Y^2－1)／Y^4・(sinθ)^2
　　　　 ＝－{Ｙ－（３＋２√２）}{Ｙ－（３－２√２）}（Y^2－1)／Y^4・(sinθ)^2
ここで、Ｙは交点Ａのｙ座標であり
π/2＜θ＜πの時、Ｙ＞３　（図を考えれば明らか(^_^;））
またこの時、sinθ＞０である。

よって、ｄＳ/ｄθは
Ｙ＜（３＋２√２）で正
Ｙ＝（３＋２√２）で０　　
Ｙ＞（３＋２√２）で負
となる。

　また図より、θがπ/2＜θ＜πで増加するとき、Ｙは単調に減少する。
（厳密に言えば、ここも証明が要りそうです。）

　だからｄＳ/ｄθは、
αを、e^(-ｒcosα)＝３＋２√２を満たす値として
θ＜αで負、θ＝αで０、θ＞αで正となる。

（増減表を書きたいのですが、これもパソコン上では描けませんm(__)m）
　これらより、Ｓ(θ)はθ＝αで最小値をとる。
この時、ａ＝tanα＝ｒsinα/ｒcosα
　　　　　　　   ＝{e^(-ｒcosα)－３}/ｒcosα

そして、e^(-ｒcosα)＝３＋２√２より
　     ｒcosα＝log(1/( ３＋２√２))＝log(３－２√２)

 よって求めるaの値は2√2／log(３－２√２)

(終わり)


★２Ｓ（θ）＝∫ｒ（φ）^2ｄφ
（積分区間がθから（θ＋π）までの定積分）と書ける

これは、極座標形式での面積計算の基本となる式です。
ｘｙ平面において、(ｘ、ｙ）＝（ｒcosθ、ｒsinθ）となるように極座標を取るとき、

方程式：ｒ＝ｒ（θ）で表される曲線のうち、
α≦θ≦β（０≦α＜β＜２πとします）
に対応する部分と、

座標の原点Ｏを始点として、θ方向に伸びる＝つまり、Ｏから無限遠点に向かう方向が、
エックス軸の正方向から左回りにみて角θをなす＝
２本の半直線
Ｌ１：θ＝α
Ｌ２：θ＝β

で囲まれる図形の面積をＳとすると

２Ｓ（θ）＝∫ｒ（θ）^2ｄθ
（積分区間がαからβまでの定積分）＝積分

となります。これは、２本の半直線

Ｌ（φ）：θ＝φ
と
Ｌ（φ＋ｄφ）：θ＝φ＋ｄφ

及び方程式：ｒ＝ｒ（θ）で表される曲線のうち、
φ≦θ≦φ＋ｄφに対応する部分とで囲まれた部分の面積を、
半径ｒ（φ）、中心角ｄφの扇形の面積で近似し、
和をとっていることに相当します。