この前はどうも有難うございました。
おかげさまで難なく理解する事が出来ました。
今回は、今週の週末課題として出されているプリントからの出題なんで
すけど、毎週月曜日に週テストというものがあり、80点未満は再テスト
を受けなければならないというとてもおっかないものがあります。
ずっと考えてみても、全然理解できません。
で、質問は2問あります。
1、平面上の3点P1(0,0),P2(4,0),P3(0,3)を
中心として、半径がそれぞれr1,r2,r3の3つの円があり
、どの2円もちょうど1つの共有点をもっている。
このような半径の組(r1,r2,r3)をすべて求めよ。
2、2辺の長さが1と2の長方形と1辺の長さが2の
正方形の2種類のタイルがある。縦2、横nの長方形の
部屋をこれらのタイルで過不足なく敷きつめることを考える。
そのような並べ方の総数をAnで表す。ただしnは正の整数である。
たとえば、A1=1,A2=3,である。次の問いに答えよ。
(1)A3を求めよ。
(2)n≧3のとき、AnをAn-1,An-2を用いて表せ。
(3)Anをnで表せ。
考えたんですけど、全然分かりません。
宜しくお願いします。
問1
直角三角形の3辺の比3:4:5より、斜辺は5となる。
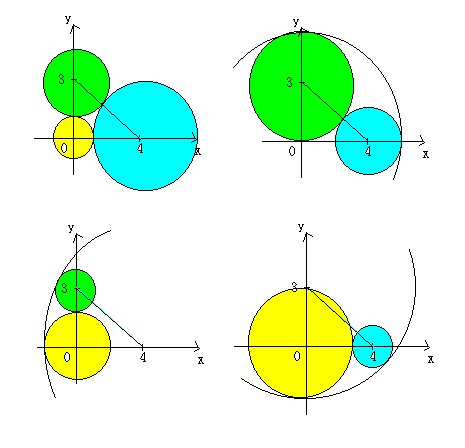
考えられる3円は、上の4通りの図のようになるので、それぞれ連立を
解いて、
{r1 +r2 =4
{r1 +r3 =3
{r2 +r3 =5
より、r1 =1,r2 =3,r3 =2
{r1 -r2 =4
{r1 -r3 =3
{r2 +r3 =5
より、r1 =6,r2 =2,r3 =3
{r2 -r1 =4
{r1 +r3 =3
{r2 -r3 =5
より、r1 =2,r2 =6,r3 =1
{r1 +r2 =4
{r3 -r1 =3
{r3 -r2 =5
より、r1 =3,r2 =1,r3 =6
したがって、
半径の組(r1 ,r2 ,r3 )
=(1,3,2)
=(6,2,3)
=(2,6,1)
=(3,1,6) ……(答)
問2
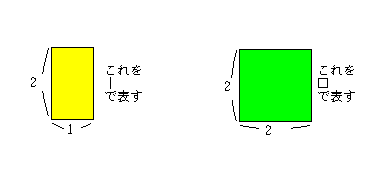
縦2、横nの長方形に上のタイルを敷き詰める問題である。Anはタイル
の並べ方の総数を指すとすると、

したがって、次のような数列ができあがる。第1階差をとると
① ② ③ ④ ⑤
1 3 5 11 21
V V V V V
2 2 6 10
幻の0番法では出来ない。多分整関数ではなく、指数関数となるのだろう。
いろいろ調べてみると、(多分難しいときは、フィボナッチ数列のような数
列だと見通しをつけて)
21-11=10=2・5
11- 5= 6=2・3
5- 3= 2=2・1
An+2-An+1=2・An
(3項の漸化式)
ただし、A1 =1、A2 =3
質問<278>の特性方程式の公式より、
An =ρn とおくと、
ρn+2-ρn+1=2・ρn
ρn+2-ρn+1-2・ρn =0
ρn (ρ2 -ρ-2)=0
特性方程式(ρ2 -ρ-2)=0より、
(ρ-2)(ρ+1)=0
∴ρ=-1,2
ρ1 ≠ρ2 より、
An =C1 (-1)n +C2 2n
A1 =1より、-C1 +2C2 =1
A2 =3より、 C1 +4C2 =3
2式を足すと、6C2 =4
C2 =4/6=2/3
-C1 +2(2/3)=1より、C1 =1/3
したがって、
1 2
An =─・(-1)n +─・2n
3 3
(-1)n +2n+1
=───────── ……(答)
3