「積分法とその応用」 - 質問＜３６２＞

質問＜３６２＞

「「積分法とその応用」」

日付２０００／１１／１９

質問者安藤正人

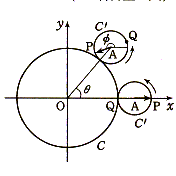
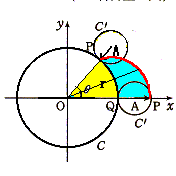
図のように、複素数平面上に原点を中心とする半径１の円Ｃと、
中心ＡがＣの外側の正の実軸上にある別の円Ｃ’があり、実軸
上の１点で外接している。Ｐ、ＱをＣ’の円周上の点として、初め
ＱはＣとの接点の位置に、ＰはＣ’と実軸とのもう一方の交点の
位置にあるとする。いまＣ’が、Ｃと接しながら滑らずに、Ａが初
めて虚軸に達するまで反時計回りに回転する。この間、点Ｐは
１度だけＣの円周と接して最後にＡＰベクトルが初めと同じベク
トルとなった。

（１）円Ｃ’の半径をｒとする。Ａが虚軸に達するまでにＣ’がＣの
　　　円周と接する部分の弧の長さをｒを用いて表せ。
　　　次にｒの値を求めよ。
（２）ＰがＣの円周に接するときのＰを表す複素数の偏角を求めよ。
（３）初めの位置からのＡＰベクトルの回転角をφ、Ａを表す複素数
　　　の偏角をθとする。φとθの関係を求めて点Ｐを表す複素数
　　　の極形式をθで表せ。
（４）Ｐが、最初の位置から、初めてＣの円周に接するまでに描く軌
　　　跡と、Ｃの円周、および実軸で囲まれる領域の面積を求めよ。

ちなみに答えは、
　　　　　　３　　　　　　１
（１）順に　―πｒ　、ｒ＝―
　　　　　　２　　　　　　３
　　　π　　　　　π　
（２）―　〔または―＋２ｎπ（ｎは定数）〕
　　　３　　　　　３
（３）φ＝４θ、点Ｐを表す複素数の極形式は、
　　　絶対値をｒ、偏角をθ’とするとｒ（ｃｏｓθ’＋ｉｓｉｎθ’）
　　　ただし
　　　　　\(\sqrt{\quad}\)（１７＋８ｃｏｓ３θ）　　　　　　　４ｃｏｓθ＋ｃｏｓ４θ
　　　ｒ＝―――――――――───、ｃｏｓθ’＝―――――――――──
　　　　　　　　　　３　　　　　　　　　　　　　\(\sqrt{\quad}\)（１７＋８ｃｏｓ３θ）

　　　　　　　　　４ｓｉｎθ＋ｓｉｎ４θ
　　　ｓｉｎθ’＝―――――――――──
　　　　　　　　　\(\sqrt{\quad}\)（１７＋８ｃｏｓ３θ）

　　　１１
（４）――π
　　　５４

できたら明日の夜までにお願いします。
なるべく詳しく解く過程を教えてください。

お返事（武田）

日付２０００／１１／２２～２７

回答者武田

問１

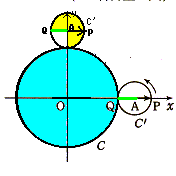
点Ａが虚軸に移動したとき、点Ｑは円Ｃ′の円周の長さ２πｒの３／４
回転したことになるから、
　　　　３　３πｒ
２πｒ・─＝───　……（答）
　　　　４　　２
また、そのとき、円Ｃで考えると、９０°移動したことになるから
２π・１・１／４＝π／２
したがって、
３πｒ　π　　　　　１
───＝─より、ｒ＝─　……（答）
　２　　２　　　　　３

問２

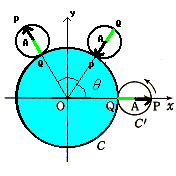
点Ｑがもう一度円Ｃと接するのは、円Ｃ′が１回転したところだから、
長さは
　　　　　　　１　２
２πｒ＝２π・─＝─π
　　　　　　　３　３
円Ｃは半径が１だから、円周の長さ＝角度となる。
点Ｐが円Ｃに接するのは、点Ｑが円Ｃに接するところの丁度半分だから、　　２　　　　π
θ＝─π÷２＝─　……（答）
　　３　　　　３

問３
　　π　　　　　　４
θ＝─ならば、φ＝─π
　　３　　　　　　３

　　π
θ＝─ならば、φ＝２π
　　２

　　２　　　　　　　８
θ＝─πならば、φ＝─π
　　３　　　　　　　３
より、
φ＝４θ……①

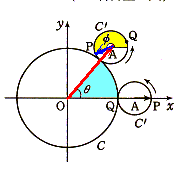
点Ａの複素数は
　　　　　　　　　　　　　　　　　　４
Ｚ_oa＝（１＋ｒ）（cosθ＋ｉsinθ）＝─（cosθ＋ｉsinθ）
　　　　　　　　　　　　　　　　　　３
ベクトルＡＰの複素数は、①より、
　　　　　　　　　　　　　　１
Ｚ_ap＝ｒ（cosφ＋ｉsinφ）＝─（cos４θ＋ｉsin４θ）
　　　　　　　　　　　　　　３
したがって、
複素数の和より、
Ｚ_op＝Ｚ_oa＋Ｚ_ap
　　　４　　　　　　　　　　１
　　＝─（cosθ＋ｉsinθ）＋─（cos４θ＋ｉsin４θ）
　　　３　　　　　　　　　　３

　　　１　　　　　　　　　　　　１
　　＝─（４cosθ＋cos４θ）＋ｉ─（４sinθ＋sin４θ）
　　　３　　　　　　　　　　　　３

Ｚ_op＝ｒ（cosθ′＋ｉsinθ′）とすると、
　　\(\sqrt{\quad}\)｛（４cosθ＋cos４θ）²＋（４sinθ＋sin４θ）²｝
ｒ＝──────────────────────────
　　　　　　　　　　　　　３

　　\(\sqrt{\quad}\)｛１６＋８（cosθcos４θ＋sinθsin４θ）＋１｝
　＝────────────────────────
　　　　　　　　　　　　　３

　　\(\sqrt{\quad}\)｛１７＋８cos（θ－４θ）｝
　＝──────────────
　　　　　　　　３

　　\(\sqrt{\quad}\)（１７＋８cos３θ）
　＝──────────　……（答）
　　　　　　３
したがって、
　　　　　（４cosθ＋cos４θ）
cosθ′＝───────────　……（答）
　　　　　\(\sqrt{\quad}\)（１７＋８cos３θ）

　　　　　（４sinθ＋sin４θ）
sinθ′＝───────────　……（答）
　　　　　\(\sqrt{\quad}\)（１７＋８cos３θ）

問４

極座標による面積は次の公式となる。
ｒ＝ｆ（θ）のとき
　　　θ₂１
Ｓ＝∫　　─・ｒ²ｄθ
　　　θ₁２

したがって、面積Ｔは
　　π/3　１　　　\(\sqrt{\quad}\)（１７＋８cos３θ）
Ｔ＝∫　　─・（　──────────　）²ｄθ
　　０　　２　　　　　　　３

　　　１　π/3
　＝──・∫　（１７＋８cos３θ）ｄθ
　　１８　０

　　　１　　　　　　８　　　　　π/3
　＝──・［１７θ＋─・sin３θ］
　　１８　　　　　　３　　　　　０

　　　１　　１７π
　＝──・（───＋０－０－０）
　　１８　　　３

　　１７
　＝──π
　　５４

円Ｃの面積Ｕは
　　　　　　　　６０°　π
Ｕ＝π・１²・────＝─　だから、
　　　　　　　３６０°　６

問題の面積Ｓは
　　　　　　１７　　１　　１７－９　　　８　　　４
Ｓ＝Ｔ－Ｕ＝──π－─π＝────π＝──π＝──π　……（答）
　　　　　　５４　　６　　　５４　　　５４　　２７

　　　　１１
※正解の──πと違うので、どこか間違っているのだろうか？
　　　　５４

お便り

日付２００２／１２／１６

回答者 charliebrown

お久しぶりです。
かなり昔の質問362の(4)の解答が質問者の答えと異なっている理由がわかり
ましたので投稿します。

解答では極座標による面積の公式を用いて計算しています。この公式自体は
間違っていないのですが、この問題に適用する際に誤りが生じてしまいました。
積分の∫\(r^{2}\)dθは、曲線上の点Pを(r,θ)の極形式で表した時のrとθです。
そのため、この問題で正しく公式に当てはめるには、Pの偏角はθではなくθ'
になるのです。それをθのまま計算したので、計算結果にずれが生じたのです。
この公式をもちいてあえて計算をするならば、θ'で一度積分を表してから、
(3)の結果を用いて、θの積分に置換しなければなりません。そして、置換後の
積分は結構複雑です。（僕もまだ解いていませんが）
代わりに、x軸にそって積分する従来の方法を用いると、Pの軌跡の下側（軌跡と
x軸と直線x=\(\frac{1}{2}\)に囲まれた部分）の面積は∫ydx（積分区間は[\(\frac{1}{2}\),\(\frac{5}{3}\)]）となり
ます。これを(3)の結果を用いて積分変数をθに置換して計算し、扇形や三角形
の面積を足し引きすると、正しく11π/54が得られます。