[1]aは実数とする。連立方程式
ax+(a-1)y=1........①
(a+1)x+ay=3.......②
を解け。
[2]実数x,yが
-1≦x+y≦1、-1≦x-y≦5
を満たすとき、z=3x+yのとりうる値の範囲を求めよ。
[3]a<0,b<0,c<0,a+b+c=1のとき、
a3+b3+c3の最小値を求めよ。
(a3はaの三乗のこと)
[4]任意の実数aに対して、2つの曲線
y=ax2-2x+2a+n+1
y=x2-4ax-a+2n-1
が常に共有点を持つときの整数nの個数を求めよ。
(ax2はaxの二乗のこと)
[5]実数x,yがx2+y2≦8を満たすとき、
X=x+y,Y=x2+y2-8
とするとき、点(X,Y)の存在する領域の面積を
求めよ。
(x2はxの二乗のこと)
問1
ax+(a-1)y=1........①
(a+1)x+ay=3.......②
①×a-②×(a-1)より
{a2 -(a2 -1)}x=a-3(a-1)
∴x=-2a+3……③
③を①に代入して、
a(-2a+3)+(a-1)y=1
(a-1)y=2a2 -3a+1
=(a-1)(2a-1)
a≠1のとき、y=2a-1
したがって、
a≠1のとき、
{x=-2a+3
{y=2a-1 ……(答)
問2
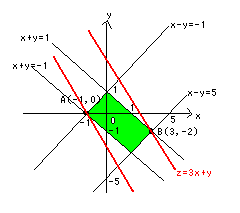
z=3x+yにおいて、
A(-1,0)を通るとき、最小値をとるから
z=-3
B(3,-2)を通るとき、最大値をとるから
z=9-2=7
したがって、
-3≦z≦7 ……(答)
問3
a<0,b<0,c<0なのに、a+b+c=1とは変ですね。
不等号のどれかは間違っていませんか?
a3 +b3 +c3 -3abc=(a+b+c)(a2 +b2 +c2 -ab-bc-ca)
1
=─(a+b+c){(a-b)2 +(b-c)2 +(c-a)2 }
2
(a+b+c)>0,(a-b)2 ≧0,(b-c)2 ≧0,(c-a)2 ≧0より、
a3 +b3 +c3 -3abc≧0
a3 +b3 +c3 ≧3abc
したがって、
最小値は3abc(a=b=cのとき)……(答)
問4
{y=ax2 -2x+(2a+n+1)
{y=x2 -4ax+(-a+2n-1)
が共有点を持つのは、連立した解があることだから
(a-1)x2 +(4a-2)x+(-3a+n-2)=0……①
①の判別式D/4≧0より、
(2a-1)2 -(a-1)(-3a+n-2)≧0
7a2 -(5+n)a+(n-1)≧0……②
②の不等式が、すべての実数aに対して成り立つためには
②の判別式D≦0だから、
(5+n)2 -4・7・(n-1)≦0
n2 -18n+53≦0
n=9\(\pm\)2\(\sqrt{\quad}\)7より、
9-2\(\sqrt{\quad}\)7≦n≦9+2\(\sqrt{\quad}\)7
3.72……≦n≦14.28……
整数で考えると、
4≦n≦14
個数は14-4+1=11個……(答)
問5
{x2 +y2 ≦8……①
{X=x+y……②
{Y=x2 +y2 -8……③
②を変形して、y=X-x
これを③に代入して、
Y=x2 +(X-x)2 -8=2x2 -2Xx+X2 -8
2x2 -2Xx+(X2 -8-Y)=0
解の公式より、
X\(\pm\)\(\sqrt{\quad}\){X2 -2(X2 -8-Y)}
x=─────────────────
2
X\(\pm\)\(\sqrt{\quad}\)(-X2 +2Y+16)
=────────────── ……④
2
実数xより、\(\sqrt{\quad}\)の中は≧0となるから
-X2 +2Y+16≧0
1
Y≧─X2 -8……⑤
2
y=X-xに④を代入して
X\(\pm\)\(\sqrt{\quad}\)(-X2 +2Y+16)
y=X-────────────── ……⑥
2
④と⑥を①に代入して計算すると、Y≦0……⑦
⑤と⑦より、
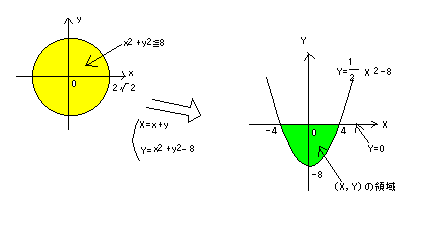
面積は定積分で求めると、
4 1
S=-∫ (──X2 -8)dX
-4 2
X3 4 64 64
=-[ ─ -8X] =-(───-32)+(-───+32)
6 -4 6 6
128 -128+384 256 128
=-───+64=────────=───=─── ……(答)
6 6 6 3