図のように、正三角形ABCの外接円の孤BC上の任意の点をPとする。
このとき
AP=BP+CP
が成り立つことを証明せよ
って問題なんですが
解答がたくさんあるらしいんですがトレミー以外思いつきません
もしよければほかの解き方も教えてください
★希望★完全解答★
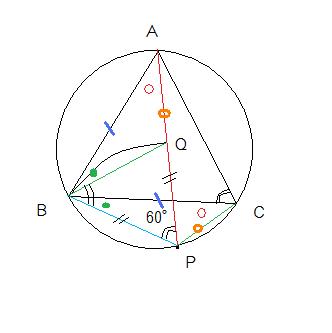
中学数学的かもしれませんが
AP上にPBと等しい長さをPから取りその点をQとします。
円周角の定理から角APBは60°です。
つまり60°を挟む二辺が等しいので三角形PBQは正三角形です。
そのひとつの角QBPは60°なので角ABQ=角CBPとなります。
(60°から角QBCという同じ角をひくから)
また円周角の定理より角BAQ=角BCP,
辺AB=辺BCより三角形ABQ≡三角形CBP。
よってAQ=CP。
よってAQ+QB=AQ+QP=CP+PB。
というのも解法のひとつでは。