次の球面やトーラスや射影平面などの任意の閉曲面は、必ず３角分割できるので、

問題の多面体は、球面と位相同型なので、３角分割できる。

「オイラーの多面体定理」は、多面体において３角分割したとき、
頂点の個数ｖ、辺の個数ｅ、３辺形の個数ｆとすると、
オイラー標数＝ｖ－ｅ＋ｆ＝２となる。

これを高校生にも分かるように証明するとなると、数学的帰納法が良い
と思います。
「多面体のオイラー標数は２となる」を証明しよう。

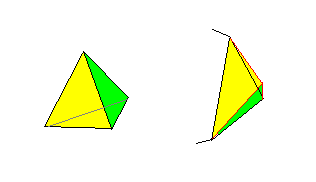
（１）ｖ＝４の場合は、３角分割すると、四面体となる。
　　　　　　ｖ＝４、ｅ＝６、ｆ＝４より、
　　　　　　オイラー標数＝ｖ－ｅ＋ｆ＝４－６＋４＝２
（２）ｖ＝ｎのとき、３角分割して、オイラー標数が２となると仮定すると、
　　　　　　ｖ＝ｎ、ｅ＝ａ、ｆ＝ｂとすると、
　　　　　　オイラー標数＝ｖ－ｅ＋ｆ＝ｎ－ａ＋ｂ＝２
　　　ｖ＝ｎ＋１のときは、ｖ＝ｎの多面体の１つの面上に１点を取ると良いから、
　　　　　　ｖ＝ｎ＋１、ｅ＝ａ＋３、ｆ＝（ｂ－１）＋３＝ｂ＋２より、
　　　　　　オイラー標数＝ｖ－ｅ＋ｆ
　　　　　　　　　　　　＝（ｎ＋１）－（ａ＋３）＋（ｂ＋２）
　　　　　　　　　　　　＝ｎ－ａ＋ｂ＋１－３＋２
　　　　　　　　　　　　＝ｎ－ａ＋ｂ＋０　←仮定より
　　　　　　　　　　　　＝２
したがって、（１）（２）より、
ｎ≧４の自然数ｎの頂点をもつ多面体は、オイラー標数が２となる。