こんにちは。ぷりんです。夏休みの遊びすぎで実力テストが40点前後に
なりました(;_;)大変大変!ではでは質問させてください。
①xy平面上に原点0と点P(a,b),点Q(x,y)の3点をとる。またベクトル
pはベクトルOPでベクトルqはベクトルOQとする。
(1)|ベクトルp|=1となる点Pを第一象限に1つ固定するとき,
ベクトルpとベクトルqの内積が1以下になる点Qの存在する範囲を
図示せよ。
(2)|ベクトルp|=1となる全ての点Pに対して
ベクトルpとベクトルqの内積が1以下になる点Qの存在する範囲を
図示せよ。
②数列{A(n)}についてA(1)=1,A(n+1)=ルート【2+A(n)】『nは
自然数』が成り立つとする。
(1)すべてのnについて0<A(n)<2が成り立つことを,nに関する
数学的帰納法で示せ。
(2)A(n)=2cosθ(n)『nは自然数』とおくとき,θ(1)を求め,
θ(n+1)をθ(n)を用いて表せ。ただし0°<θ(n)<90°『nは自然数』
とする。
(3)一般項A(n)を求めよ。
よろしくおねがいします。
問1
(1)
→ →
p=(a,b)、q=(x,y)とすると、
内積が1以下より、
→ →
(p,q)=ax+by≦1………①
①より、
ax+by=1は、原点が中心、半径1の円の円周上の点P(a,b)における
接線の方程式だから
点Qの存在範囲は、図のようになる。

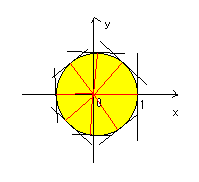
(2)
→
点Pが|p|=1となるすべての点をとるとき、内積が1以下となるのは、
b>0において、接線より下部
b<0において、接線より上部
b=0のとき
a>0において、接線より左側
a<0において、接線より右側
以上のすべての共通部分が点Qの存在範囲だから
図のようになる。
問2
(1)
a1=1
an+1=\(\sqrt{\quad}\)(2+an)
(nは自然数)
「すべてのnについて、0<an<2が成り立つ」ことを
数学的帰納法で証明すると、
(i)n=1のとき、a1=1より、0<a1<2
(ⅱ)n=kのとき、0<ak<2が成り立つと仮定して、
n=k+1のとき、
ak>0より、2+ak>0
ak+1=\(\sqrt{\quad}\)(2+ak)>0
ak+1を2乗して、
(ak+1)2=2+ak<2+2=4
ak+1>0より、
ak+1<\(\sqrt{\quad}\)4=2
∴0<ak+1<2
したがって、(i)(ⅱ)より、すべてのnについて、与式が成り立つ。
(2)
an=2cosθnとおくと、
a1=2cosθ1=1
0°<θn<90°より、
1 π
cosθ1=――より、θ1=―― ………(答)
2 3
an+1=\(\sqrt{\quad}\)(2+an)より、
2cosθn+1=\(\sqrt{\quad}\)(2+2cosθn)
2乗して
4cos2θn+1=2+2cosθn
2cos2θn+1-1=(1+cosθn)-1
cos2θn+1=cosθn
2θn+1=θn
1
∴θn+1=―θn ………(答)
2
(3)
1
∴θn+1=―θn
2
1
=(―)n・θ1
2
π 1
=―・(―)n
3 2
したがって、
an=2cosθn
π 1
=2cos{――・(――)n-1} ………(答)
3 2