はじめまして。次の問題教えてください。参考書を見ても
よくわかりません。テストがあさってにあるので、できるだけ
早くお願いします。
<問1>
直線l:x=-1,点F(1,0)がある。点P(x,y)からlに垂線PHを
ひくとき、e=PF/PHを考える。
(1)e=1/\(\sqrt{\quad}\)2のとき、点Pの軌跡を求めよ。
<問2>
楕円x^\(\frac{2}{9}\) + \(y^{2}\)/4=1の第一象限の部分の上に点P(x,y)をと
る。点PからX軸、Y軸にそれぞれ垂線PQ,PRをひく。
長方形OQPRの面積の最大値とそのときのPの座標を求めよ。
よろしくお願いします。
<問1>
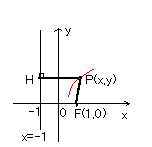
P(x,y)とF(1,0)間の距離は、PF=\(\sqrt{\quad}\){(x-1)2+y2}
P(x,y)とH(-1,y)間の距離は、PH=x+1
PF/PH=e=1/\(\sqrt{\quad}\)2より、
\(\sqrt{\quad}\){(x-1)2+y2} 1
────────=────
x+1 \(\sqrt{\quad}\)2
変形して
\(\sqrt{\quad}\)2×\(\sqrt{\quad}\){(x-1)2+y2}=x+1
2乗して
2{(x-1)2+y2}=(x+1)2
展開して
2x2-4x+2+2y2=x2+2x+1
x2-6x+1+2y2=0
x2-6x+9-9+1+2y2=0
(x-3)2+2y2=8
したがって
(x-3)2 y2
─────+───=1
8 4
点Pの軌跡は、中心(3,0)、長径2\(\sqrt{\quad}\)2、短径2の楕円となる。
<問2>

楕円x2/9 + y2/4=1の第一象限の部分の
長方形OQPRの面積をSとする。
S=xy
2乗して
S2=x2y2……①
x2/9 + y2/4=1を変形して
y2=4-\(\frac{4}{9}\)・x2……②
②を①に代入すると、
S2=x2y2
=x2(4-\(\frac{4}{9}\)・x2)
=4x2-\(\frac{4}{9}\)・x4
=-\(\frac{4}{9}\)(x4-9x2)
=-\(\frac{4}{9}\)(x4-9x2+\(\frac{81}{4}\)-\(\frac{81}{4}\))
=-\(\frac{4}{9}\)(x2-\(\frac{9}{2}\))2+9
x2=\(\frac{9}{2}\)のとき、最大値9
点P(x、y)は第一象限だから、x>0より、
∴x=3/\(\sqrt{\quad}\)2
②に代入して、
y2=4-\(\frac{4}{9}\)・\(\frac{9}{2}\)=4-2=2
y>0より、
∴y=\(\sqrt{\quad}\)2
点P(3/\(\sqrt{\quad}\)2、\(\sqrt{\quad}\)2)
S>0より、面積の最大値は
S=\(\sqrt{\quad}\)9=3