それともうひとつ教えてください。
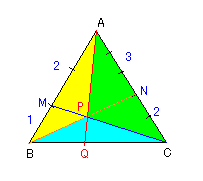
△ABCにおいて線分ABを2:1に内分する点をMとし
線分ACを3:2に内分する点をNとするまた2つの線分
CMとBNとの交点をPとし直線APと辺BCとの交点をQとする
次の問いに答えよ
(A)3つの三角形の面積比、△ABP:△BCP:△CAPを求めよ
→ → →
(B)ベクトルAQを2つのベクトルAB、ACで表せ
→ → →
(C)ベクトルAPを2つのベクトルAB、ACで表せ
よろしくお願いします。
問1
チェバの定理より、
2 BQ 2
―・――・―=1
1 QC 3
BQ 3
――=―
QC 4
BQ:QC=3:4
メネラウスの定理より、
7 QP 2
――・――・―=-1
-4 PA 1
QP 2
――=―
PA 7
QP:PA=2:7
△ABP:△BPQ=BQ・AP:BQ・QP
=3・7:3・2
=21:6
△CAP:△CPQ=CQ・AP:CQ・QP
=4・7:4・2
=28:8
△BCP=△BPQ+△CPQ=6+8=14
△ABP:△BCP:△CAP=21:14:28
=3:2:4 ………(答)
問2
―→ ―→
―→ 4・AB+3・AC 4 ―→ 3 ―→
AQ=―――――――――=―・AB+―・AC ………(答)
3+4 7 7
問3
メネラウスの定理より、
5 NP 3
――・――・―=-1
-3 PB 4
NP 4
――=―
PB 5
NP:PB=4:5
―→ ―→
―→ 4・AB+5・AN 4 ―→ 5 ―→
AP=―――――――――=―・AB+―・AN
4+5 9 9
―→ 3 ―→
AN=―・AC より、
5
―→ 4 ―→ 5 3 ―→
AP=―・AB+―・―・AC
9 9 5
4 ―→ 1 ―→
=―・AB+―・AC ………(答)
9 3