なんだかパラドックスに陥りそうです。HELP・・
\(x^{2}\)+\(\frac{2}{x}\) の最小値を求めよ、という問題。
1)\(x^{2}\)+\(\frac{2}{x}\)
=\(x^{2}\)+\(\frac{1}{x}\)+\(\frac{1}{x}\)
>=3(\(x^{2}\)*\(\frac{1}{x}\)*\(\frac{1}{x}\)\()^{1}\)/3 (相加相乗平均)
=3
よって最小値は3
2)\(x^{2}\)+\(\frac{2}{x}\)
>=2(\(x^{2}\)*\(\frac{2}{x}\)\()^{1}\)/2 (相加相乗平均)
=2(2x\()^{1}\)/2---1式
等号成立はx~2=\(\frac{2}{x}\)よりx=\(2^{1}\)/3
これを1式に代入して
最小値は\(2^{5}\)/3
1)が正しくて2)が間違っているのはなんとなくわかるのですが、
なぜ2)が間違いなのかをうまく説明できません。
また2)のやり方も和が一定などの条件があれば使えるようなのですが
これもよくわかりません。
教えてくださ~い
\(y=x^{2}+\frac{2}{x}\) をグラフの合成より、
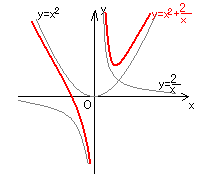
相加相乗平均は、正の実数を扱うから、x>0の範囲で考えると、
1)の場合は、図のようにy=3との接点だから
x=1のとき、最小値3となる。
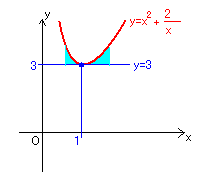
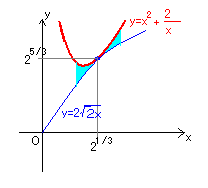
2)の場合は、図のように \(y=2\sqrt{2x}\) との接点だから
\(x=^{3}\sqrt{2}\) のとき、 \(y=^{3}\sqrt{2^{5}}\) となるが、最小値ではない。
したがって、
相加相乗平均
\(a_{1},a_{2}\) は、正の実数のとき、 \(\frac{a_{1}+a_{2}}{2}\geq \sqrt{a_{1}a_{2}}\)
\(a_{1}=a_{2}\) のとき、最小値が求まると言うより、
相加平均と相乗平均が等しくなる言った方がよいだろう。
ただし、右辺の相乗平均が定数で表現できたときは、最小値となる。