まず、線分PQの中点をOとすると、
点Oは線分PQと線分ARを二等分するので、四角形APRQは平行四辺形です。
点Rが△ABCの外になるか、中になるかで場合分けをします。

PQ//BC で、
AP
--＝t とおくと、0＜t＜1で、
AB
AP：AB＝t：1 ですから、
t＝\(\frac{1}{2}\) のとき、点Rが線分BC上になります。

(i)0＜t≦\(\frac{1}{2}\) のとき
点Rは△ABCの内部（または辺上）にあり、
△PQRは△ABCにすっかり含まれるので、
共通部分の面積Sは、△PQRの面積に他なりません。
ところが、△PQR≡△APQですから、
Sは、△APQの面積で求まります。
△APQ∽△ABCで、相似比はAP：AB＝t：1 ですから、
面積比は\(t^{2}\)：1となり、△ABC＝1 から、
S＝\(t^{2}\)
となります。

(i)\(\frac{1}{2}\)＜t＜1 のとき
点Rは△ABCの外部にあります。
線分PR、QRと辺BCとの交点をそれぞれD、Eとすると、
△ABCとの共通部分は台形PDEQになります。
四角形APRQが平行四辺形なので、
AP＝QR、したがってQR：AB＝t：1。
また、PB//QE、PQ//BEより、四角形PBEQは平行四辺形で、
PB＝QEより、QE：AB＝(1-t)：1。
よって、
RE：AB＝(QR-QE)：AB＝(2t-1)：1。
△RQP、△REDはどちらも△ABCと相似ですから、
(i)の時と同様に面積は相似比の2乗で求まり、
△RQP＝\(t^{2}\)、△RED＝(2t-1\()^{2}\) となります。
ゆえに、
S＝△RQP-△RED＝\(t^{2}\)-(2t-1\()^{2}\)＝-3\(t^{2}\)+4t-1
です。
横軸t、縦軸Sでグラフを描くと、2つの放物線がt＝\(\frac{1}{2}\)でなめらかにつながり、
S＝-3\(t^{2}\)+4t-1の頂点(t＝\(\frac{2}{3}\))で最大値\(\frac{1}{3}\)を取ることがわかります。

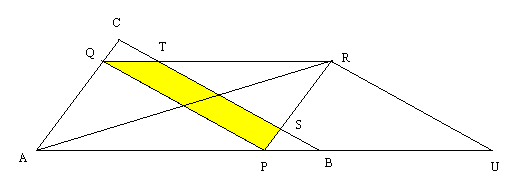
図にあるように APRQ は平行四辺形になる。
AB:AP を 1:x としよう。
0 ≦ x ≦ \(\frac{1}{2}\) では
S = \(x^{2}\) (相似比の自乗)
だから単調増加である。
\(\frac{1}{2}\) ＜ x ≦ 1 の時,
図の AB:BU = 1: (2x -1) なので
S = △PRQ - △PST = \(x^{2}\) - (2x-1\()^{2}\)
= \(x^{2}\) - (4\(x^{2}\) - 4x + 1)
= -3\(x^{2}\) + 4x - 1
= -3(x - \(\frac{2}{3}\)\()^{2}\) + \(\frac{1}{3}\).
だから x - \(\frac{2}{3}\) の時最大で最大値は \(\frac{1}{3}\).