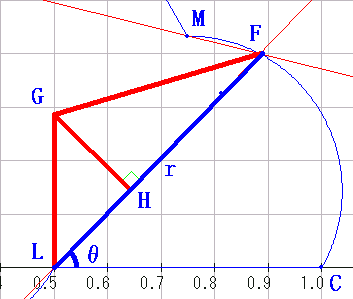
一辺の長さが1の正三角形ABCがある。辺BC,辺CA、辺ABの
中点をそれぞれL、M,Nとし
AP=BQ=CR=t
となる辺AB上の点をP,辺BC上の点をQ,辺CA上の点をRとし、
直線PM、直線QN,直線RLをそれぞれm1、m2、m3とする。
m1とm2、m2とm3、m3とm1との交点をそれぞれD,E,F
とし、三角形DEFを考える。
このときtが0から1まで変化するとき、三角形DEFが通過する領域
を図示しその面積を求めよ。
この問題がわかりません。
お手数ですがなるべくお早めに回答よろしくお願いします
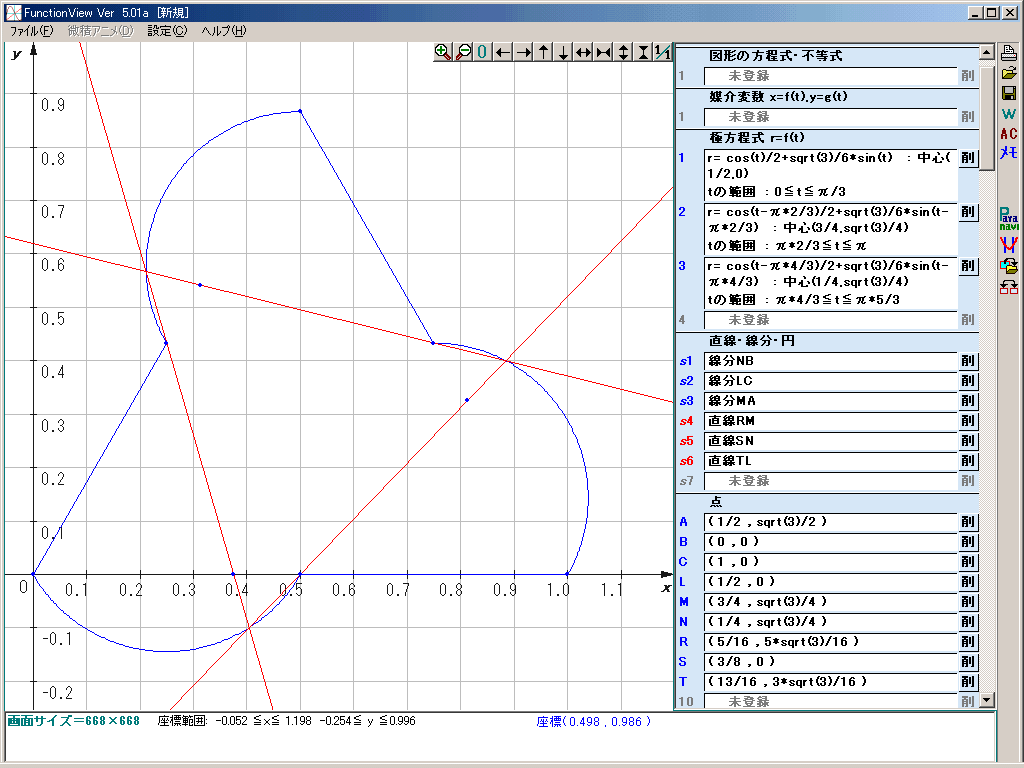
図の青線で囲まれた部分が求める領域です。
(赤線は三角形DEFの例です。)
曲線部分は極方程式の形式で記述することができます。
面積を計算すると、π/12+(3\(\sqrt{\quad}\)3)/16 となるでしょう。
(計算ミスをしている可能性もありますので、あまり信用しないよう。)