質問＜１０５＞９８／１２／２４
こんにちは、なぜ数学１・Ａの三角比で四角形の問題が出る のですか？ という質問をした倉本達也というものです。 数学は中学２年までは得意科目の一つでした。 しかし、学区割りの変更に伴う中学校転校をした中学３年生 のとき、非常に横柄で、しかも他の中学問題を自ら出してお きながら「おれはｘｘ中学校の先生じゃないから分からない」 という恐ろしく非常識な発言をしていた教員に出会ってしま ってからは、数学が嫌いになり大学入試でも数学を使わず私 立大学の法学部に進学しました。 しかし、マンモス私大法学部の退屈さの中、入学前うすうす 考えていたように生物学領域を専攻したいと思うようになり ました。現在は出来れば医学部、学力的に難しければ理学部 入学を考えています。 それゆえ独学で勉強をしていたのですが、ことし３度目のセ ンター型模擬試験で初めて四角形の問題が出たので、自分が 数学１の範囲を勘違いしていたのかと思い、かなり衝撃を受 けました。 以下に問題を書きます。 駿台予備校１９９８年センタープレ試験数学１・Ａ 第２問 ｛２｝ 円に内接する四角形ＡＢＣＤがありＡＢ＝ＢＣ＝３ ＣＤ＝４ である。 （１）ＡＤ＝７のとき ∠Ａ＝（シス）° ＢＤ＝√（セソ） △ＡＢＣの外接円の半径＝√（タチツ）／（テ） である。 （２）ＡＣ、ＢＤの交点をＥとする。ＥがＡＣの中点のとき ＡＤ＝（ト） ＢＥ＝（ナ）／（ネ） である。 以上。 正直言って数学が中学２年まで得意だったわりに、図形分野 をものの見事に忘れていたようです。 「四角形を分割する２つの三角形にできる」ということを忘 れていたのですから。 ”中点”も中点連結定理とかいうのがあったようなないような.. 予備校の模範解答をみても 「三角形２つを合体させて１つの四角形を作れる」 などといった事は書いてないので数学１の範囲のどこかに平 面幾何があったのかと思いずっと、書店などで本をにらんで ました。 三角比は図形がらみの出題なので個人的に好きではないです。 関数のように数式とグラフの問題が勉強しやすいです。 よろしければ三角比をするうえで重要な図形の定理などを 教えていただきたいです。 以上。
お返事９８／１２／２５
from=武田
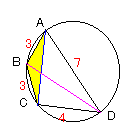
問２（１）△ＡＢＤと△ＣＢＤにおいて、ＢＤを求める余弦定理より ３2＋７2－２・３・７cosＡ＝３2＋４2－２・３・４cos（１８０°－Ａ） cosＡ＝１／２∴∠Ａ＝６０°……（答） ＢＤ2＝３2＋７2－２・３・７・（１／２） ＝３７ ∴ＢＤ＝√３７……（答） △ＡＢＣと△ＡＣＤにおいて、ＡＣを求める余弦定理より ３2＋３2－２・３・３cosＢ＝７2＋４2－２・７・４cos（１８０°－Ｂ） cosＢ＝－４７／７４ 公式sin2θ＋cos2θ＝１より sinＢ＝√｛１－（－４７／７４）2｝ ＡＣ2＝３2＋３2－２・３・３・（－４７／７４） ＝１０８９／３７ ＡＣ＝√（１０８９／３７） △ＡＢＣにおける正弦定理より、 ２Ｒ＝ＡＣ／sinＢ ＝√（１０８９／３７）／√｛１－（－４７／７４）2｝ ∴Ｒ＝√（１１１）／３……（答） 問２（２）
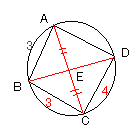
△ＡＢＥと△ＣＢＥにおいて、ＡＢ＝ＢＣ＝３、点ＥはＡＣ の中点よりＡＥ＝ＣＥ ＢＥは共通。したがって△ＡＢＥ≡△ＣＢＥ したがって対角線ＢＤとＡＣは直交する。 円の弦ＡＣに対する垂直二等分線ＢＤと円の交点Ｄは二等辺 三角形△ＤＣＡを作るから、 ∴ＡＤ＝ＣＤ＝４……（答） △ＡＢＤと△ＣＢＤにおいて、ＢＤを求める余弦定理より ３2＋４2－２・３・４cosＡ＝３2＋４2－２・３・４cos（１８０°－Ａ） cosＡ＝０∴∠Ａ＝９０°
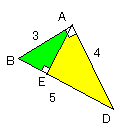
△ＡＢＤは直角三角形より、３：４：５の三辺の比が成り立つ。 △ＡＢＥと△ＡＢＤにおいて、 ∠ＡＢＥ＝∠ＡＢＤ（共通） ∠ＡＥＢ＝∠ＢＡＤ＝９０° したがって△ＡＢＥ∽△ＡＢＤ ＢＡ：ＢＤ＝ＢＥ：ＢＡより ３：５＝ＢＥ：３ ∴ＢＥ＝９／５……（答）