質問＜１３７０＞２００３／８／２８
from=わく
「1/4円の重心」

半径ｒの円を4等分したときの1/4円の重心を求める

半円の重心はスレがありましたが1/4の重心を求める方法がわかりません。
よろしくお願いします。

お返事２００３／９／２
from=武田

質問＜１６３＞の半円の重心と同様にして求める。



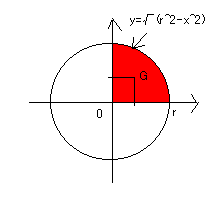
半円周の曲線の方程式が
ｙ＝√（ｒ2－ｘ2）
０≦ｘ≦ｒということで計算してみた。

１／４円の面積は
Ｍ＝∫∫　ｄｘｄｙ
　　　Ｄ

　x=r　　　y=√（ｒ2－ｘ2）
＝∫　ｄｘ　∫　ｄｙ
　x=0　　　y=0

　ｒ
＝∫　√（ｒ2－ｘ2）ｄｘ
　０

　π/2
＝∫　ｒcosθ・ｒcosθｄθ
　０

＝πｒ2／４

１／４円の面積は二重積分を使わなくても簡単に出せましたね。

重心は図より、
＿
ｙ＝∫∫　ｙ　ｄｘｄｙ　／Ｍ
　　　Ｄ

　x=ｒ　　　y=√（ｒ2－ｘ2）
＝∫　ｄｘ　∫　ｙｄｙ　／Ｍ
　x=０　　　y=0

　ｒ
＝∫　（ｒ2－ｘ2）／２　ｄｘ　／Ｍ
　０

　　　　　　　　　ｒ
＝【ｒ2ｘ－ｘ3／３】　／２Ｍ
　　　　　　　　　０

　２ｒ3　１
＝──・──
　３　　２Ｍ

　４ｒ
＝──
　３π

＿
ｘも同様にして、

したがって、
　　　４ｒ　４ｒ
点Ｇ（──，──　）……（答）
　　　３π　３π

お便り２００３／９／３
from=Tetsuya Kobayashi

半円の重心が分かれば四分円の重心はすぐ分かるような気もしますが…。
xy 平面で、原点中心半径 r の円の x,y>=0 の部分について考えます。
重心の x 座標を c と置けば、明らかに重心の y 座標は c です。
重心の定義により、
∫[0..r](c-x)√(r^2-x^2)dx = 0
ですから、これをしこたま計算すれば c=4r/(3π) を得ます。