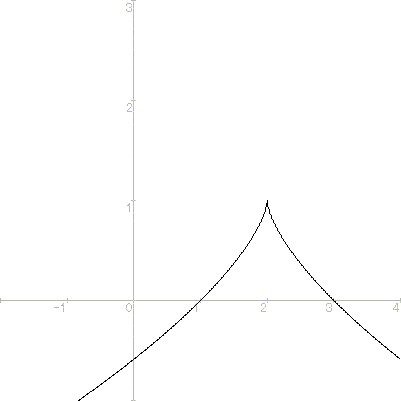質問＜１８＞９８／６／１９
from=坂田
「微分可能」

なぜ微分可能なら連続であるのに、連続であっても、
微分可能とは限らないのですか？
具体的に教えて下さい。

お返事９８／６／２０
from=武田

定理「f(x)が区間Ｉにおいて微分可能ならば、f(x)は区間Ｉにおいて連続である。」
【証明】
区間Ｉの中のx=aにおいて微分可能ならば、
lim　f(a+h)-f(a)＝f'(a)であるから、
h→0　　　h
f(a+h)-f(a)＝f'(a)+εとおくと、
　　h
f(a+h)-f(a)＝h×{f'(a)+ε}、ここでh→0のときはε→0
∴lim　｛f(a+h)-f(a)｝＝０
　h→0
a+h=xとおくと、h→0のときx→a
lim　｛f(x)－f(a)｝＝０
x→a
lim　f(x)＝f(a)
x→a
したがって、区間Ｉの中のx=aにおいて連続となる。

逆は成り立たない。
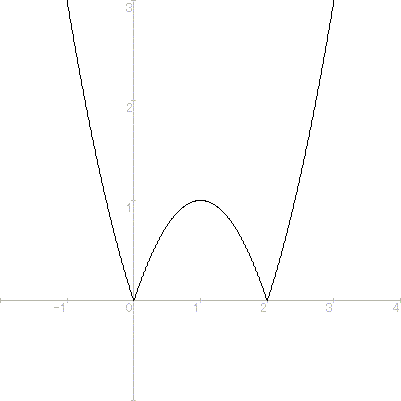
例えば、f(x)＝｜2x-x2｜のx=2においては連続だが、
左方微分係数が－２、右方微分係数が２と異なるので、微分可能ではない。

他に、f(x)＝1-(x-2)2/3のx=2においても同様である。