こんにちは!「かっち」です。
先日はどうもありがとうございました。
今日もまた分からない問題があったので力になっていただけ
ないかとメールしました。
どうかよろしくお願いします。
問題 : 半径の等しいn個の円C1,C2,…,Cnが
半径1の円Cに内接し、C1とC2,C2とC3,…,
Cn-1とCn,CnとC1がそれぞれ外接しているものと
する。半径の等しいn個の円の半径をRnとするとき、以下
の問いに答えよ。
(1)lim(nRn)=πを示せ。
n→∞
(2)(ア)θ>0のとき、sinθ>θ-θ(三乗)/6が
成り立つことを示せ。
(イ)(ア)を用いて、lim{n(π-nRn)}を
求めよ。 n→∞
<ヒント>
(1) Rn={sin(π/n)}/{1+sin(π/n)}
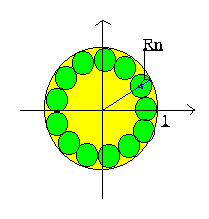
(1)内接する1つの円の幅の角度は2π/n
その真ん中を通る接線の角度はθ=2π/n÷2=π/n
接線は直角になるからsinθ=Rn/(1-Rn)
変形して、
Rn=sinθ/(1+sinθ)
=sin(π/n)/{1+sin(π/n)}
sin(π/n) π
n・Rn=────────×────────────
(π/n) {1+sin(π/n)}
sin(π/n) π
lim(n・Rn)=lim ─────×───────
n→∞ π/n→0 (π/n) {1+sin(π/n)}
=1×π/{1+0}=π……(答)
(2)(ア)は、この図には関係なくマクローリン展開から
求められる。
sinθ=θ-θ3/3!+θ5/5!-……
θ2n-1
lim (-1)n-1──────=0より、
n→∞ (2n-1)!
sinθ≒θ-θ3/3!+θ5/5!
したがって、θ>0より、
sinθ>θ-θ3/3!
∴sinθ>θ-θ3/6
この連珠の円に関連させながら、マクローリン展開を使わな
いで、この式を出すのは不明!!!
(2)(イ)(ア)を用いて、lim{n(π-nRn)}を
n→∞
求める方法について関谷先生からアドバイスを頂きました。
下に掲載します。