①関数f(x)=xe^-(\(x^{2}\))について次の問いに答えよ
ただしeは自然対数の底である。
(1)関数y=f(x)の極地、増減、変曲点、凸凹を調べ
グラフの概形をかけ。ただし
x→+∞ x→-∞ のとき、f(x)→0である。
(2)曲線y=f(x)(x≧0)とx軸および直線x=a(a>0)
で囲まれた部分の面積Saを求め、
さらに極大値 lim a→+∞ Saを求めよ
②a>0とする、直線Lが曲線C1:y=logxと
C2:y=log(x-a)+aのどちらとも接している
(1)Lの方程式を求めよ
(2)L,C1,C2 により囲まれる部分の面積S(a)を求めよ
(3)極大値 lim a→+∞ (S(a)/\(a^{2}\)) を求めよ
ただし、lim a→+∞ (log\(\frac{x}{x}\)) =0を用いても良い
③m,nは0または正の整数とする。
定積分 Im,n=∫from 0 to 1 {\(x^{m}\)・(1-x\()^{n}\)・dx}について次の問いに答えよ
(1)n≧1のとき、Im,n=(\(\frac{n}{m}\)+1)・Im+1,n-1を示せ
(2)Im,nを求めよ
(3)S=Σ r=0~n {\(a^{r}\)・(1-a\()^{n}\)-r/Ir,n-r}を求めよ
ただし0<a<1 (aは定数)とする。
今回は難しい問題が連続したことと、家族全員が夏風邪にやられたことが
原因で、解答が遅くなりました。やっと完成しました。ヤレヤレ!
問1
(1)
f(x)=xe-\(x^{2}\)
f′(x)=e-\(x^{2}\)+xe-\(x^{2}\)・(-2x)
=e-\(x^{2}\)(1-2x2 )
f″(x)=e-\(x^{2}\)(-2x)(1-2x2 )+e-\(x^{2}\)(-4x)
=e-\(x^{2}\)(-2x+4x3 -4x)
=e-\(x^{2}\)(4x3 -6x)
増減表とグラフを描いてみると、
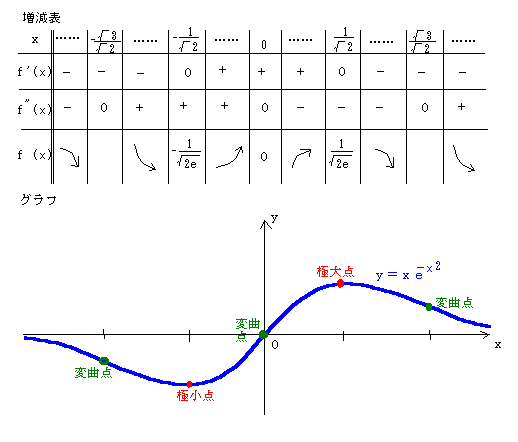
(2)
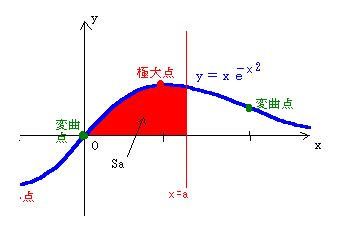
Sa=∫0axe-\(x^{2}\)dx
置換積分を使って解くと、
-x2 =tとおくと、
-2xdx=dt
x|0→a
t|0→-a2
1
Sa=-─∫0-\(a^{2}\)etdt
2
1
=-─[et]0-\(a^{2}\)
2
1
=-─(e-\(a^{2}\)-e0)
2
1
=─(1-e-\(a^{2}\)) ……(答)
2
したがって、
1
lim Sa=─ ……(答)
a→∞ 2
問2
(1)
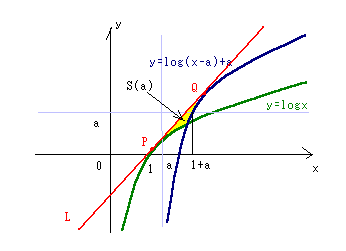
対数関数y=logx上の接点P(x1 、y1 )とすると、
y′=1/xより、
y1 =logx1
接線Lの方程式は
y-logx1 =1/x1 (x-x1 )
これがもう一つの対数関数y=log(x-a)+aと接するから
y′=1/(x-a)より、
1/(x-a)=1/x1
x1 =x-a
x=x1 +a
これを代入して、
y=log(x1 +a-a)+a
=logx1 +a
したがって、もう一つの接点Q(x1 +a,logx1 +a)を接線Lに代入すると、
logx1 +a-logx1 =1/x1 (x1 +a-x1 )
a=a/x1
∴x1 =1
P(1,0)、Q(1+a,a)
y-0=1(x-1)より、
接線L:y=x-1 ……(答)
(2)
2つの対数関数の交点は連立より、
{y=log(x-a)+a
{y=logx
logx=log(x-a)+a
x
log───=a
x-a
x
───=ea
x-a
x=xea -aea
x(ea -1)=aea
aea
∴x=────
ea -1
したがって、囲まれた面積S(a)は2つの部分の積分の和となるから
S(a)=∫1 a\(e^{a}\)/(\(e^{a}\)-1){(x-1)-logx}dx
+∫a\(e^{a}\)/(\(e^{a}\)-1)1+a{(x-1)-log(x-a)-a}dx
途中の計算が大変なので、省略して
1 a
S(a)=-─a2 +alog|────| ……(答)
2 ea-1
(3)
S(a) 1 1 a
────=-─ +─log|────|
a2 2 a ea -1
1 loga log(ea -1)
=-─+────-─────────
2 a a
logx
lim────=0より、
x→∞ x
loga log(ea -1)
lim────=0、lim─────────=0
a→∞ a a→∞ a
したがって、
S(a) 1
lim ────=-─ ……(答)
a→∞ a2 2
問3
(1)
左辺=Im,n
=∫0 1 xm(1-x)ndx
xm+1 xm+1
=[────(1-x)n ]0 1 -∫0 1 ────・n(1-x)n-1 (-1)dx
m+1 m+1
n
=0-0+───∫0 1 xm+1 (1-x)n-1 dx
m+1
n
=───・Im+1,n-1=右辺
m+1
(2)
n n-1
Im,n=───×───×Im+2,n-2
m+1 m+2
n n-1 n-2 1
=───×───×───×……×───×Im+n,0
m+1 m+2 m+3 m+n
m!n!
=─────・∫0 1 xm+n dx
(m+n)!
m!n! xm+n+1
=─────・[─────]0 1
(m+n)! m+n+1
m!n!
=──────── ……(答)
(m+n+1)!
(3)
n ar (1-a)n-r
S=Σ ─────────
r=0 Ir,n-r
n ar (1-a)n-r
=Σ ─────────
r=0 r!(n-r)!
────────
(n+1)!
n
=Σ (n+1)n Cr ar (1-a)n-r
r=0
n
=(n+1)Σ n Cr ar (1-a)n-r
r=0
=(n+1){a+(1-a)}n
=n+1 ……(答)