質問<76>で同じ質問をされている方がいますが、
そのお返事にあるように確かに球の体積を微分したら球の表面積になりました。
でも、体積と同じように円周2πrをxについて積分してみると
S=2∫2π\(\sqrt{\quad}\)(\(r^{2}\)-\(x^{2}\))dx (0からrまで)
x=rsinθ とおくとdx=rcosθdθ となり
S=2∫2πrcosθ rcosθ dθ (0からπ/2まで)
=4π\(r^{2}\)∫(cosθ\()^{2}\)dθ
=2π\(r^{2}\)∫(cos2θ+1)dθ
=2π\(r^{2}\)[(sin2θ)/2+θ]
=2π\(r^{2}\) π/2
=(πr\()^{2}\) となって4π\(r^{2}\)になりません。
なにか根本的間違いがあるのでしょうか?
★希望★完全解答★
いま円錐の例で考えてみよう。
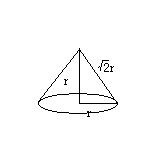
体積は円錐の公式より、(1/3)πr^3
これを回転体の積分で求めると、π∫(0,r)y^2dx
r
y=xより、π∫(0,r)x^2dx=π[x^3/3] =(1/3)πr^3
0
ところが、側面積を扇形の展開図から求めると、
2πr
π(\(\sqrt{\quad}\)2r)^2・―――――――=\(\sqrt{\quad}\)2πr^2
2π(\(\sqrt{\quad}\)2r)
ベーコンさんのやり方で求めると、2π∫(0,r)ydx
r
y=xより、2π∫(0,r)xdx=2π[x^2/2] =πr^2
0
となって、異なる答えが出ます。
これは、円盤を重ねて求めた体積とは違って、円周に微小な線分の長さを
掛けて求めていくという表面積独特のやり方があるのです。
公式はこうなります。
b dy
S=2π∫ y\(\sqrt{\quad}\){1+(――)^2}dx
a dx
^^^^^^^^^^^^^^^^^^
↑
この部分が微小な線分の長さにあたります。
これを使って、上の円錐の表面積を求めると、
r dy
S=2π∫ y\(\sqrt{\quad}\){1+(――)^2}dx
0 dx
y=xより、dy/dx=1
r
S=2π∫ x\(\sqrt{\quad}\){1+(1)^2}dx
0
r
=2\(\sqrt{\quad}\)2π[x^2/2] =\(\sqrt{\quad}\)2πr^2
0
したがって、球の表面積は、
y=\(\sqrt{\quad}\)(\(r^{2}\)-\(x^{2}\))より、
dy/dx=-2x/2\(\sqrt{\quad}\)(\(r^{2}\)-\(x^{2}\))
=-x/\(\sqrt{\quad}\)(\(r^{2}\)-\(x^{2}\))
\(\sqrt{\quad}\){1+(dy/dx)^2}=\(\sqrt{\quad}\){r^2/(r^2-x^2)}
=r/\(\sqrt{\quad}\)(r^2-x^2)
S=2∫2π\(\sqrt{\quad}\)(\(r^{2}\)-\(x^{2}\))・r/\(\sqrt{\quad}\)(r^2-x^2)dx (0からrまで)
=4πr∫dx(0からrまで)
=4πr[x](0からrまで)
=4πr^2 ……(答)