質問

以下のような条件の体積を求めなければならなくなりました。
積分を使うのが、王道と思いますが、切り口が楕円？になるようで、式が求められません。
目的は、高さｈのときの体積が知りたくExcelを使用して結果を求める予定です。
Excelで求められるところまで解答頂ければ助かります。
急ですみませんが、17日までに解答頂けるとさらに助かります。

---
半径rの円柱を、地表面に角度θになるように傾ける。
円柱の両端を長さLになるように、長さ方向と、地表面に垂直に切断し蓋をした。
この円柱に水を注いだときの、高さhにおける、水の体積は？。

　　　／|
　　／　|
　／　／
 |　／
 |／

★希望★完全解答★

お便り２００６／４／１６
from=ZELDA

この問題に関しては、あまり自信がないので、質問された方にお願いがあります。
これを読んで正しいか確認してください。間違っていたら、教えてください。
そのときは、もう一度チャレンジしてみます。

それと、どこの長さがLなのかよくわからなかったので、間違っている場合には、
教えてください。私は円柱を切断する2平面の距離がLであるとして解答を書きます。

(解答)円柱と地面との交点をAとする。また、底面の円の中心に関するAの対称点
をBとする。ここで、2底面の円の中心を通り、かつ、地面に垂直な平面で円柱を
切断したときにできる長方形で、四角形ABCDとなるように、点Cと点Dを定める。

このとき、円柱を、Aを通り問題にあるような平面で切断する。これによってできる
立体のうちBを含むものを立体Bと呼ぶ。（平面と直線BCの交点をEとする。）
また、もう一方をCを通り問題にあるような平面する。これによってできる立体の
うちDを含むものを立体Dと呼ぶ。
（平面と直線ADの交点をFとする。）

地面に立てた垂線と2底面の円の中心を通る直線のなす角は、θである。
このとき、直線CFと直線ADのなす角は、θである。
AF=L/sinθ
DF=2L/tanθ
円柱の底面の半径がrであるから、
（もとの円柱の体積）=πr^2*AD=πr^2(AF+DF)
=πr^2[(L/sinθ)+(2L/tanθ)]・・・・・・・・・(1)

立体Bと立体Dを平行移動して、重ねると底面が半径rで、高さが2L/tanθの円柱になる。
（立体Bと立体Dの体積の和）
=πr^2(2L/tanθ)・・・・・・・・・・・・・・・(2)

（もとめる体積）=（もとの円柱の体積）-（立体と立体の体積の和）
=(1)-(2)
=πLr^2/sinθ　　(ただし、0＜θ＜2π)・・・・(答）

ずいぶんと長くて、まどろっこしい解答になってしまいました。
間違いがあったら、教えてください。

お便り２００６／４／１６
from=社会人

さっそく回答いただきありがとうございます。
求めて頂きたい体積、うまく表現できませんので図を作りました。



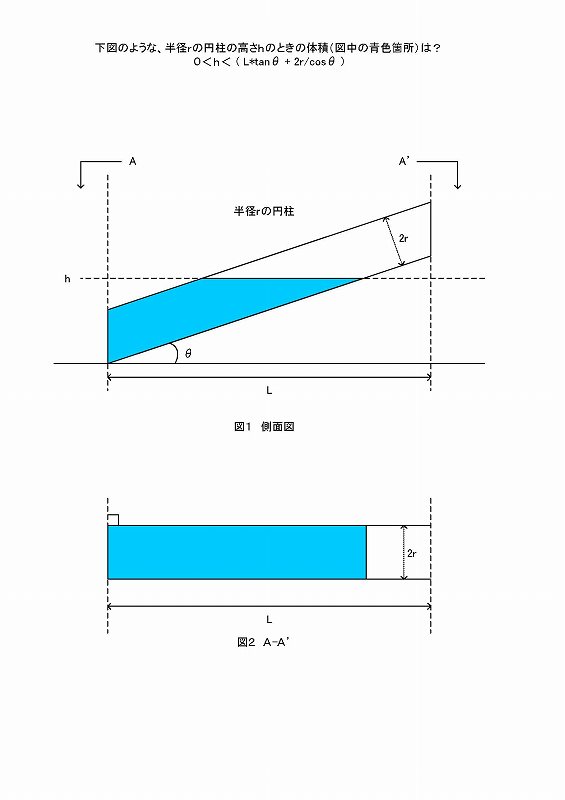
今一度、よろしくお願いいたします。

お便り２００６／４／１９
from=angel

図を見る限り、
半径 r, 高さ 2rtanθ の円柱を半分に割ったもの
半径 r, 高さ (h-2r/cosθ)/sinθ の円柱
半径 r, 高さ 2r/tanθ の円柱を半分に割ったもの
の合計に見えますね。
つまり、体積は
 πr^2・(rtanθ+r/tanθ+(h-2r/cosθ)/sinθ)=πr^2・(h/sinθ-2r/sin2θ)
尤も、2r/cosθ≦h≦Ltanθ の条件が要りますが。
※水面が半端な所になるため。

なお、円柱を半分に割ったものが、円柱の半分の体積になることは、
積分計算でも確かめられます。
※一部分だけでも、三角関数の逆関数で表すことはできます。

半径 r, 高さ h の円柱
　x^2+y^2≦r^2
　-h/2≦z≦h/2
の内、平面で半分に切断した領域は
　x≧2rz/h

断面積
　S(z)=r^2・f(2z/h)
この f(t) は、
　f(t)=π/2-arcsin(t)-t√(1-t^2)

ここで、以下の置換により体積を計算する。
　t=2z/h, dt=2/h・dz, dz=h/2・dt
　t=sinθ, dt=cosθdθ

∫[-h/2,h/2] S(z) dz
= ∫[-h/2,h/2] r^2・f(2z/h) dz
= hr^2/2・∫[-1,1] f(t)dt
= hr^2/2・∫[-1,1] (π/2-arcsin(t)-t√(1-t^2))dt
= hr^2/2・(π-∫[-1,1] (arcsin(t)+t√(1-t^2))dt )
= hr^2/2・(π-∫[-π/2,π/2] (θ+sinθcosθ)cosθdθ )
= πhr^2/2

ちなみに、
g(θ)=θcosθ+sinθ(cosθ)^2 とする時、
∫g(θ)dθ
=θsinθ-∫sinθdθ-1/3・(cosθ)^3
=θsinθ+cosθ-1/3・(cosθ)^3

お便り２００６／４／１９
from=ZELDA

社会人さんの図1の円柱の断面からできる平行四辺形で地面と接している点をAとする。
また、反時計回りにG,C,Bをとる。Gから線分BCにおろした垂線の足をHとする。

Gを原点として、→GHの向きにx軸をとる。このとき、x=xによる円柱の切断面は長方形
である。この長方形の2辺のうち、図1に垂直である辺の長さをk、円柱の高さ方向の辺
の長さをm、とする。

このとき、円柱を線分GHを通り、円柱に垂直な断面を考える。この断面は半径rの円で
あり、x=xによる断面はこの円上では、円の中心からの距離が|r-x|の弦になる。
この弦の長さがkである。
三平方の定理より、
k=2√[r^2-(r-x)^2]=2√(2rx-x^2)・・・・・(1)

(イ)0≦h≦Ltanθのとき
水面とx=xの交点をE,x=xと線分ABの交点をFとする。
m=EF=[h-(x/cosθ)]/sinθ
この式をf(x)とおく。

(ロ）Ltanθ≦h かつ　点Eが存在するとき
このとき(h-Ltanθ)/cosθ≦x
この値をβとする。
(イ)と同様に
m=EF=f(x)

(ハ）Ltanθ≦h かつ　点Eが存在しないとき
このとき0≦x≦β
また、m=GA=cosθ/L

(1),(イ)、(ロ）、(ハ)、より
求める体積をVとおくと、

0≦h≦2r/cosθのとき
V=∫[0,hcosθ]kf(x)dx

2r/cosθ≦h≦Ltanθのとき
V=∫[0,2r]kf(x)dx

h≧Ltanθのとき
V=∫[0,β](kL)/cosθdx+∫[β,2r]kf(x)dx

ただし、k=2√(2rx-x^2)
       f(x)=[h-(x/cosθ)]とする。


この解答は、GがBよりも高い位置にあるとして問題を解いてあります。図の送り方が
わからないので、図がなく、説明もうまくできず、非常にわかりにくい解答になって
しまいました。すいません。それと、これまた、あまり自信がありません。
せっかく、図まで送っていただいたのにすいません。
ところで、Excelで積分は計算できるのでしょうか？
積分は残っていて大丈夫ですか？

（※解答ありがとうございます。図の送り方ですが、管理人宛のメールに添付ファイル
　　として送って頂いても結構です。ワードでも一太郎でも、ｂｍｐでもｐｓｐでも、
　　ＴｅＸでもｐｄｆでもほとんど大丈夫です。変換してｊｐｇでホームページに掲載
　　しています。ｊｐｇで送って頂けるととっても助かります。管理人談）
　　　　→管理人への直接メールは、ここをクリック