次の関数のグラフをかけ。
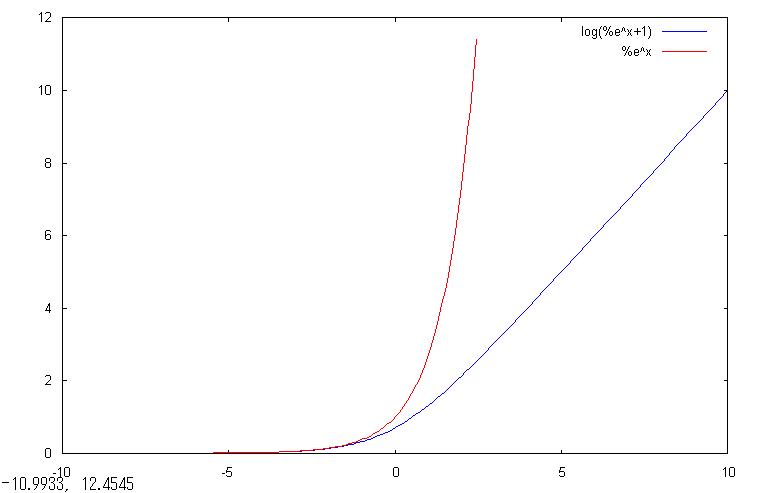
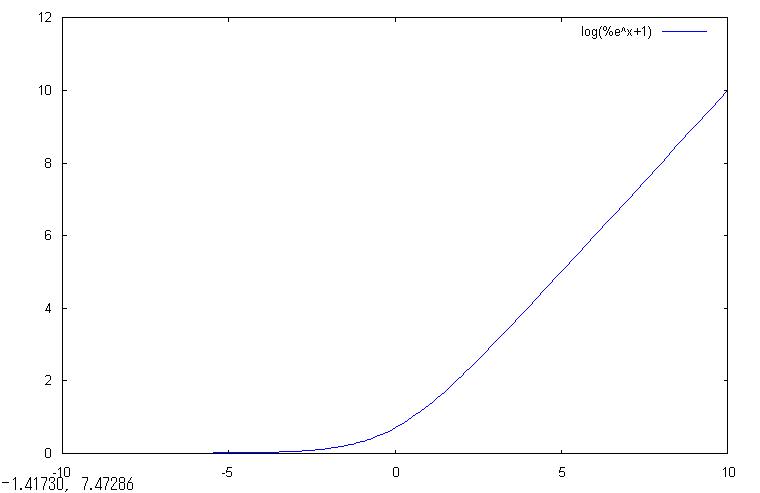
①y=log(1+\(e^{x}\))
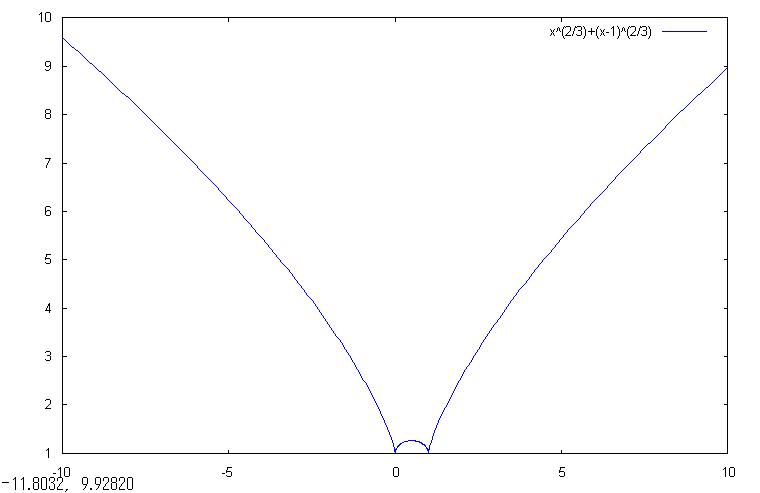
②y=\(x^{2}\)/3+(x-1\()^{2}\)/3 (指数が\(\frac{2}{3}\))
グラフの問題なのでまず導関数を求めてみたのですが、
導関数=0になるXが存在せず、グラフが描けません。
この対数関数と指数関数のグラフを描くためには、
どのような計算をしていったらよいのか教えてください。
★希望★完全解答★
ワタシは数学の事はサッパリ分からないんで何とも言えないのですが(笑)、グラフを描く
事だけは可能です。
僕はテキトーなんで(笑)、数学的な解法は他のお方にお任せするとして(笑)、取りあえず
コンピュータ上でグラフを描いてみる方法だけお教え致しましょう(と言うのも未解決問
題が多過ぎるので、取りあえず減らした方がイイと思うからです)。
以下はフリー数式処理ソフトMAXIMA(ウィンドウズ版)でのグラフ描画方法です。
まずはMAXIMAをダウンロードしてください。
MAXIMAをダウンロードしたら、デスクトップ上にMAXIMAのアイコンが
出来る筈です。それをダブルクリックして下さい。
そうすると次の画面が現れる筈です。
Maxima 5.9.3 http://maxima.sourceforge.net
Using Lisp GNU Common Lisp (GCL) GCL 2.6.7 (aka GCL)
Distributed under the GNU Public License. See the file COPYING.
Dedicated to the memory of William Schelter.
This is a development version of Maxima. The function bu\(g_{r}\)eport()
provides bug reporting information.
(%i1)
これが起動成功と言う印です。また(%i1)は入力待ち、と言った意味です(iは恐らく
input"入力"と言う意味)。
さて、MAXIMA出の描画コマンドは次のようなモノです。
plot2d(描画したい関数,[変数x,下限,上限]);
このように;(セミコロン)まで入力します。以上です。
ではちょっとやってみましょう。
>①y=log(1+\(e^{x}\))のグラフをかけ。
入力待ち記号(%i1)の後に次のように入力します。
(%i1) plot2d(log(1+exp(x)),[x,-10,10]);
今回は取りあえず-10≦x≦10の範囲で描画してみましょう。この指定が[x,-10,10]の部分です。
以上のように;(セミコロン)まで入力し終わったらリターンキーを押します。そうすると、
MAXIMAがグラフを描画してくれる筈です。
同様に、
②y=\(x^{2}\)/3+(x-1\()^{2}\)/3のグラフをかけ。(指数が\(\frac{2}{3}\))
も、
(%i2) plot2d(x^(\(\frac{2}{3}\))+(x-1)^(\(\frac{2}{3}\)),[x,-10,10]);
で描画してくれる筈です。
なお、下記に、MAXIMAでの描画グラフをお届けします。
確かに微分では描画できないような感じのグラフになっていますね。
問1
問2