質問＜３２５１＞2006/6/16
from=KAI
「統計（至急）２」
続けて投稿すみません。過去ログ見てもわからないので、質問させてください。
ある工場では１分間に平均17.5個の部品を製造していた。いま、新しい製造方法を
取り入れて部品を製造し、平常状態になったところで、無作為に12回の測定時間
（各回1分間）を選んで調べた。その結果は
20, 17, 19, 21, 20, 18, 16, 18, 21, 19, 19, 17
であった。新しい製造方法は以前よりも能率的であるといえるか危険度1%で検定せよ。
ただし、一定時間内に完成させる個数は正規分布に従うものとする。
統計がいまだによくわからないので解説お願いします。
★完全解答希望★
お便り２００６／６／１９
from=亀田馬志
＞統計がいまだによくわからないので解説お願いします。
う～ん･････参りましたねえ･･････。
いや、解説するのが不可能とは思っていないのですが、これを一から説明するとなると、
分量が･･････(笑)。
と同時に、｢統計がいまだによくわからない｣との事なんですが、極論全然構わないと思っ
ています(笑)。
と言うのも、前項でも書きましたが、｢確率･統計｣は数学ではなくって、ある意味｢データ
解析マニュアル｣なんですよね。統計学者にでもならない限り、原則的には単に和田秀樹
的に(笑)｢手順｣を把握すれば済むワケで、数学的に厳密な論理展開の把握、と言うのは
不必要です。かつそんな事は出来ないでしょう(笑)。
特に現在主流の｢標本理論｣と言う統計手法で言うと、これは基本的に｢一貫性｣とは縁の
無い手法なんです。歴史的には、色々処々の問題に付いて個別に解析手法を発展させて
来た経緯があるんで、一つの俯瞰した視点から(例えば物理学のように)全て全体を見渡
せるかどうかに付いては････多分殆どムリなんじゃないかな?その辺りを統計学者自身が
気付いているからこそ、論理的整合性に付いての論争が多く行われているワケですし、
そしてそれに付いて決着がいまだに付いていないのです。
と言うわけで、｢データ解析マニュアル｣としてはポイントだけ押えていこうと思っています。
＞ある工場では１分間に平均17.5個の部品を製造していた(一定時間内に完成させる個数
は正規分布に従うものとする)。
まずこの情報から、
(旧)1分間に製造できる製品数～N(17.5, σ^2)
とします。
｢～｣と言う記号は｢と言う分布に従う｣の簡略表現で、N（μ,σ^2)と言うのは｢母平均μ、
母分散σ^2の正規分布｣って意味ですね。正規分布の数式書くのは統計学者でもかなり
メンド臭いらしいので(笑)、こう言った簡略表記が発達してきたワケです。
現時点では母平均μは17.5と分かっていますが、母分散に付いては未知です。まずはココ
を押えておいて下さい。
＞いま、｢新しい製造方法｣を取り入れて部品を製造し、平常状態になったところで、
無作為に12回の測定時間（各回1分間）を選んで調べた。その結果は
20, 17, 19, 21, 20, 18, 16, 18, 21, 19, 19, 17
であった。
さて、今、｢旧製造方法｣を母集団として定義し、この｢新しい製造方法｣が｢旧製造方法｣と
同じか否か?と言う事を問題としているのです。
現時点、｢新しい製造方法｣のサンプルは12回しかありませんし(これを標本と呼びます)、
ここで｢新しい製造方法｣の母集団は現時点ではまだ定義できません(と言うより、難しい、
と言った方がイイのですが)。
｢新しい製造方法の母集団が定義できないのだったら、旧製造方法との差なんて論じられ
ないでしょ?｣
と言った疑念は至極もっともです。
ここでちょっと発想を変えてみます。仮に、
｢新しい製造方法｣のサンプル(標本)が、｢旧製造方法｣と言う母集団から採取されたもの
としたら･･･?
と考えるのです。
仮に、｢新しい製造方法｣のサンプル(標本)が、｢旧製造方法｣と言う母集団から採取された
ものだとしたら、平均は恐らく17.5くらいで大して変わらないでしょう。まあ、これは確
かに妥当な結論だと思います。
つまり、この｢仮に･･･｣と言った考え方を｢仮説｣として定義しなおせば良いのです。
｢新しい製造方法｣の母平均をμ新とすると、
仮説①:μ新＝μ
として数学的に定義します。
しかし、上の仮説は本当に証明したい事ではありません。問題文に拠ると、
＞新しい製造方法は以前よりも能率的である
と言う事を言いたいらしい。｢能率的｣とは何でしょうか?当然｢新しい製造方法｣での製造
個数の母平均が｢旧製造方法｣での製造個数の平均値より上回っていればイイ。
つまり、仮説②は次のようになるワケです。
仮説②:μ新＞μ
仮説②が正しいとすれば、｢新しい製造方法｣の母集団はどんなモノなのか全然分かりませ
んが、少なくとも｢旧製造方法｣の母平均よりは｢母平均がデカイ集団｣である、と言う事だ
けは言えるワケです。そしてそれは仮説①を否定できる結果が得られれば言える｢結論｣な
んです。
以上を考え合わせて、仮説①を｢帰無仮説｣、仮説②を｢対立仮説｣と呼びます。
ちょっと書き直してみましょうか?
帰無仮説:μ新＝μ
対立仮説:μ新＞μ
｢帰無仮説さえ否定できれば対立仮説が確率的に正しいと言える｣････これが｢統計的仮説
検定｣のカラクリです。
という事は、僕らがやっきになって焦点を絞るのは、
｢新しい製造方法｣のサンプル(標本平均)が、｢旧製造方法｣と言う母集団から採取された
ものである事
を頑張って証明すればイイ。そしてそれが失敗すれば｢対立仮説が確率的には正しい｣と
なるのです。ヘンな発想ですね(笑)。
さて、取りあえず｢新しい製造方法｣での標本平均x-hatを求めてみましょうか。
x-hat＝(20+17+19+21+20+18+16+18+21+19+19+17)/12
＝18.75
18.75＞17.5なので、
｢バンザイ!!!これで新しい製造方法は旧製造法よりも能率的だ!｣
メデタシ、メデタシ････とコレでイイのか?
ダメなんですね。何故なら、
＞無作為に12回の測定時間（各回1分間）を選んで
がポイントです。つまり｢18.75｣と言った数値は｢たまたま｣無作為に選んだ結果ですし、
毎回毎回この値になる、とは当然限らないでしょう。つまり言い換えると、
標本平均も分布する
のです。これがこのテの問題の難しいトコなんですね。
取りあえず｢新しい製造方法｣のデータのバラ付き具合(不偏標本分散s^2と標準偏差s)を
計算してみましょうか(公式は教科書に譲ります)。
s^2≒2.568182
s≒1.602555
なるほど。この位の量で標本平均はバラついているようです･･････だから?
｢旧製造法｣の母分散は丸っきり分からない状態でした。しかも｢新しい製造方法｣の標本数
はたったの12個で分布を定義するにもままならない･･････。
19世紀流の統計学者だったら、
｢もっと新しい製造方法でサンプルをたくさん取りなさい。そしたら何か言えるでしょう。｣
と言います。無責任もはなはだしい(笑)。八方塞がりですね。
････ところが、20世紀に入ってから、W.S.ゴセットと言うビール会社の醸造技師が革命的
な確率分布を発見したのです。それが
t分布
と言われる確率分布です(数式は教科書を参照の事)。
t分布と言うのが確率統計の教科書で恐らく一番最初に紹介される検定用の理論分布で
イマイチピンと来ない分布です。
平たく言うと、t分布とは、
標本平均のふるまいに言及した世界で初めての確率分布である
と言う事です。
ちょっとどう言う事か説明しますと、例えば｢正規分布｣と言うのは、｢データ自体の分布
の仕方｣に言及した確率分布です。これはこれでよろしい。
ただし、｢母平均μ｣を利用して定式化されているので、では、｢母平均と標本平均が必ず
しも等しいとは限らない｣状況では正規分布では何の情報も説明する事は出来ないのです。
一方t分布とは、あくまでもデータそのものではなく、｢母平均と標本平均の関連性｣に
言及した確率分布です。｢標本平均が母平均に対してどう言ったふるまいを示すのか?｣に
拘っています。よって、確率変数はデータそのものではなくって、
t＝(標本平均－母平均)/(標準偏差/√標本数)
と新しく作り出したものとなっているのです(これを検定統計量tと呼びます)。
もう一度言います。正規分布の母集団から、ランダムに数個サンプルを取り出し、そして
その情報(検定統計量t)を記録して正規分布に戻し、また取り出し、情報を記録し、また
正規分布に戻し････と言った実験を無限回行う。この場合、検定統計量tの分布がt分布と
なるのです。
これはいわゆる仮想的なシミュレーションで、と言う事は、｢t分布｣さえ知っていれば、
たった12回限りの標本平均でも、確率論的にその値の信頼性に対して言及できる、と。
それが｢統計的仮説検定｣の最初に覚えなければならないテクニックなんです。
一応検定統計量tを計算してみましょうか?標本数が12、標本平均が18.75、標本の標準
偏差が1.602555、｢旧製造方法｣の母平均が17.5、以上を鑑みると、
t＝(18.75－17.5)/(1.602555/√12)
≒9.360054
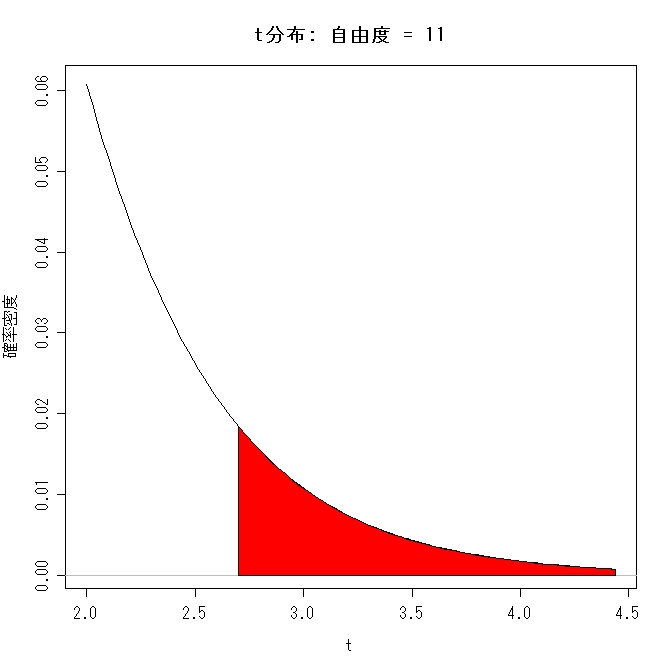
となります。このtが自由度(t分布の場合は標本数－1)11のt分布に従う確率変数となっ
ているのです。
アトはこのtがt分布上でどれだけの累積確率に対応するのか調べればイイだけなん
ですが････実は教科書によってt分布表の表記方法が違ったりします。
そこでやっぱりココではMicrosoft Excelを利用してみましょうか。しかも数表利用です
と、あんまり現代的ではないので、やはりココはP値(有意確率)での議論にした方が
トレンディでしょう。
まずはMicrosoft Excelを起動して下さい。
①A列に問題のデータを入力する。
次のようになるはずです。
| データ |
| 20 |
| 17 |
| 19 |
| 21 |
| 20 |
| 18 |
| 16 |
| 18 |
| 21 |
| 19 |
| 19 |
| 17 |
②セルA15にtと言うラベルを作る
次のようになります。
| データ | |
| 20 | |
| 17 | |
| 19 | |
| 21 | |
| 20 | |
| 18 | |
| 16 | |
| 18 | |
| 21 | |
| 19 | |
| 19 | |
| 17 | |
| | |
| t | |
③セルB15に検定統計量tの数式を入力する
次のようになります。
| データ | |
| 20 | |
| 17 | |
| 19 | |
| 21 | |
| 20 | |
| 18 | |
| 16 | |
| 18 | |
| 21 | |
| 19 | |
| 19 | |
| 17 | |
| | |
| t | =ABS(AVERAGE(A2:A13)-17.5)/(STDEV(A2:A13)/COUNT(A2:A13)) |
ここで、各Excel関数の内訳は
abs():ABS関数。絶対値を求める関数。()内の数値の絶対値を返す。
average(データ):AVERAGE関数。入力されたデータの平均値を求める。
データ範囲はセルA2～A13で、A2:A13と指定している。
stdev(データ):STDEV関数。入力されたデータの標準偏差を求める。
データ範囲はセルA2～A13で、A2:A13と指定している。
count(データ):COUNT関数。入力されたデータの個数を求める。
データ範囲はセルA2～A13で、A2:A13と指定している。
入力し終わったアト、リターンキーを押せば
t＝9.360054459
と先ほど手計算で求めた値になるのが分かると思います。
Excel関数は不慣れかもしれませんが、｢定義式通りに入力している｣事を確認しておいて
下さい(絶対値だけは、Excelの性質の為に敢えて付けてありますが)。
④セルA16にP値と言うラベルを作る。
次のようになります。
| データ | |
| 20 | |
| 17 | |
| 19 | |
| 21 | |
| 20 | |
| 18 | |
| 16 | |
| 18 | |
| 21 | |
| 19 | |
| 19 | |
| 17 | |
| | |
| t | 9.360054459 |
| P値 | |
⑤セルB16にP値の計算式を入力する。
次のようになります。
| データ | |
| 20 | |
| 17 | |
| 19 | |
| 21 | |
| 20 | |
| 18 | |
| 16 | |
| 18 | |
| 21 | |
| 19 | |
| 19 | |
| 17 | |
| | |
| t | 9.360054459 |
| P値 | =TDIST(B15,COUNT(A2:A13)-1,1) |
ここでExcel関数の内訳は、
tdist(検定統計量t,自由度,検定形式):TDIST関数。与えられた検定統計量と自由度に
従ってt分布上の累積確率の値を計算する。ここで検定統計量tは③で計算されたセルB15
を、自由度はデータ数－1をcount(データ範囲)－1として計算している。また、検定形式
では1.片側検定、2:両側検定として指定している。
なお、ここで、片側検定とは対立仮説が＞＜等と言った不等号で表現されたもの、そして
両側検定とは対立仮説が≠で表現されたもの、を指します(取りあえずはそう覚えておけ
ばイイです)。
今回は対立仮説:μ新＞μなので、1を入力しています。
⑥リターンキーを押して検定終了。
次のようになります。
| データ | |
| 20 | |
| 17 | |
| 19 | |
| 21 | |
| 20 | |
| 18 | |
| 16 | |
| 18 | |
| 21 | |
| 19 | |
| 19 | |
| 17 | |
| | |
| t | 9.360054459 |
| P値 | 7.12865E-07 |
P値が7.12865×10^(-05)％でこれは問題文に拠る有意水準(危険率)
危険度1%で検定せよ(有意水準は1％)
より遥かに小さい値
7.12865×10^(-05)％＜1％
なので、
｢新しい製造方法｣での標本平均は｢旧製造法｣での母集団から取られた標本とは思えない。
むしろそれよりも大きい母平均を持つ集団から取られた可能性が高い
となり、帰無仮説を棄却して対立仮説を採択します(逆に言うと、P値＞有意水準だと何も
結論出来なくなります)。
ゆえに、結論としては、
99％の確率で、新しい製造方法は以前よりも能率的である
となります。
以上です。
お便り２００６／６／２１
from=亀田馬志
おっとすみません。ケアレスミスしてました(苦笑)。
＞t＝(18.75－17.5)/(1.602555/√12)
≒9.360054
と書いてましたが、ルート取るの忘れてましたね(涙)。
正解は
t＝(18.75－17.5)/(1.602555/√12)
≒2.702015
です。
つまり、Excel上でのコードも書き間違いで、tの部分は
=ABS(AVERAGE(A2:A13)-17.5)/(STDEV(A2:A13)/sqrt(COUNT(A2:A13)))
になります。
SQRT関数(平方根を取る関数)を付け加え忘れていました。すいません。
アトの作業は同じですが、P値が計算では
P値≒0.01029125
となり、微妙に1％を上回っています。
従って、帰無仮説棄却は出来なくって、結論は、
｢新しい製造方法｣は古い製造方法に比べて能率的である、とは言えない。
専門的には
統計的に差は有意ではない
となります。
結論180度違っちゃいましたね。すみませんでした。
お便り２００６／６／２１
from=亀田馬志
グラフをお送りします。
それぞれのグラフの説明は以下の通りです。
＞自由度11のt分布と危険率1％の上側確率
今回の検定のように～より大きいと言う場合は、図のように
t分布上の右側の累積確率が問題となります。
Microsoft Excelのように検定統計量tを絶対値で計算する
場合、数値に特に変わりはありませんが、図示する場合図の
ように「右側か左側かそれとも両側か?」が大変重要です。
この問題のような場合、通称「右側検定」と呼びます。
また、～より小さい、と言った場合、「左側検定」と言います。
通常の平均値の検定の場合「両側検定」と呼びます。
＞有意水準拡大図
危険率が1％とかなり小さいので、有意水準の拡大図です。
＞有意確率拡大図
今度はP値(有意確率)の拡大図です。
＞有意水準と有意確率の大きさの比較
上の二つの図を重ね合わせるのが視覚化した「検定作業」です。
微妙に赤の確率(面積)＝有意確率(P値)が青の確率(面積)＝
危険率(有意水準)を上回っている事が分かると思います。
これが
P値＞有意水準
で帰無仮説が棄却できない条件なのです。