０＜ｘ＜２πのとき、
ｋｅ^{\(\sqrt{\quad}\)3x}＝cosｘの解の個数を求めるために、変形して、

　　cosｘ
ｋ＝───＝ｅ^{-\(\sqrt{\quad}\)3x}・cosｘ
　　ｅ^{\(\sqrt{\quad}\)3x}
左辺と右辺をそれぞれｙとおき、
｛ｙ＝ｋ
｛ｙ＝ｅ^{-\(\sqrt{\quad}\)3x}・cosｘ
この２つのグラフの交点を調べる。
まず、ｙ＝ｅ^{-\(\sqrt{\quad}\)3x}・cosｘを微分して、
ｙ′＝－\(\sqrt{\quad}\)３ｅ^{-\(\sqrt{\quad}\)3x}・cosｘ－ｅ^{-\(\sqrt{\quad}\)3x}・sinｘ
　　＝－ｅ^{-\(\sqrt{\quad}\)3x}（\(\sqrt{\quad}\)３cosｘ＋sinｘ）
　　＝－２ｅ^{-\(\sqrt{\quad}\)3x}・sin（ｘ＋π／３）
ｙ′＝０より、
ｅ^{-\(\sqrt{\quad}\)3x}＞０より、sin（ｘ＋π／３）＝０
０＜ｘ＜２πより、
　　２　　５
ｘ＝─π，─π
　　３　　３
代入して、
ｆ（０）＝ｅ^{-\(\sqrt{\quad}\)3・０}・cos０＝１
ｆ（２π／３）＝ｅ^{-\(\sqrt{\quad}\)3(2π/3)}・cos（２π／３）
　　　　　　　＝（－１／２）ｅ^{-2\(\sqrt{\quad}\)3π/3}
　　　　　　　≒－０．０１３
ｆ（５π／３）＝ｅ^{-\(\sqrt{\quad}\)3(5π/3)}・cos（５π／３）
　　　　　　　＝（１／２）ｅ^{-5\(\sqrt{\quad}\)3π/3}
　　　　　　　≒０．００００５８
ｆ（２π）＝ｅ^{-\(\sqrt{\quad}\)3(2π)}・cos（２π）
　　　　　＝ｅ^{-2\(\sqrt{\quad}\)3π}
　　　　　≒０．００００１９
増減表
ｘ　｜　０｜………｜２π/3｜………｜５π/3｜………｜　２π　｜
──────────────────────────────
ｙ′｜　　｜　－　｜　０　｜　＋　｜　０　｜　－　｜　　　　｜
──────────────────────────────
ｙ　｜　１｜　減少｜　※１｜　増加｜　※２｜　減少｜ｅ^{-2\(\sqrt{\quad}\)3π}｜
※１＝（－１／２）ｅ^{-2\(\sqrt{\quad}\)3π/3}
※２＝（１／２）ｅ^{-5\(\sqrt{\quad}\)3π/3}


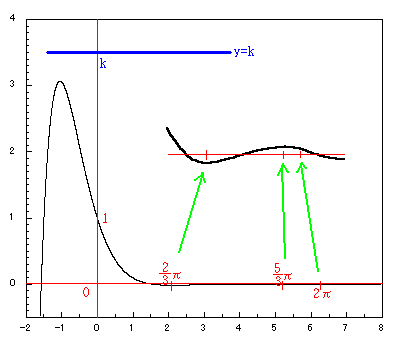
したがって、
０＜ｘ＜２πの範囲で、ｋの値によって解の個数が決まる。
｛１≦ｋのとき、解の個数０個
｛（１／２）ｅ^{-5\(\sqrt{\quad}\)3π/3}＜ｋ＜１のとき、１個
｛ｋ＝（１／２）ｅ^{-5\(\sqrt{\quad}\)3π/3}のとき、２個
｛ｅ^{-2\(\sqrt{\quad}\)3π}＜ｋ＜（１／２）ｅ^{-5\(\sqrt{\quad}\)3π/3}のとき、３個
｛（－１／２）ｅ^{-2\(\sqrt{\quad}\)3π/3}＜ｋ≦ｅ^{-2\(\sqrt{\quad}\)3π}のとき、２個
｛ｋ＝（－１／２）ｅ^{-2\(\sqrt{\quad}\)3π/3}のとき、１個
｛ｋ＜（－１／２）ｅ^{-2\(\sqrt{\quad}\)3π/3}のとき、０個　……（答）