ミクロ経済学の基本なのですが、どうしても理解できないのでお教えください。
(1)は需要Dの価格弾力性ηの定義です(Pは価格)。
ηを定数とするとき(4)式まで変形したいのですが、
(2)から(3)にいく過程がよく分かりません。
(2)ではdPやdDが変数だったのに、(3)では積分記号に変わっています。
それとも本来f(x)を積分するとはf(x)にdxを掛けるという意味なのでしょうか?
初歩的な質問ですみませんがよろしくお願いいたします。
η=-(dD/D)/(dP/P) ..........(1)
-η(dP/P)=(dD/D) ..........(2)
-η∫dP/P=∫dD/D ..........(3)
-ηlog|P|+C=log|D| ..........(4)
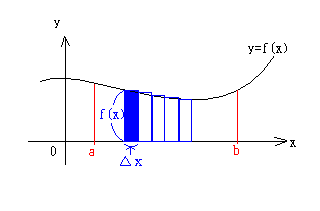
積分は、一般に「微分の逆計算(原始関数を求める)」と言われていま
すが、もともとは区分求積法から出来た方法です。
図のように、区分求積法とは、面積を細分化して、細長い長方形を無数
作り、その面積を多数加えて、全体の面積を求めると言う方法です。
細長い長方形の1つは、縦f(x)で横△x(これは、aからbまでを
n等分したもの)だから、その面積は積f(x)・△xとなる。
これをaからbまで加えていくと、
x=b
Σ f(x)・△x
x=a
しかし、まだ階段状なので、本当の面積と誤差がある。それを無くする
のが、極限の考えである。lim である。
△x→0
b-a
△x=─── より、n→∞としても良い。
n
したがって、面積は次のような式となる。
x=b
lim Σ f(x)・△x
△x→0x=a
これを後年の数学者達が積分の記号へと進化させていったのです。
b
∫ f(x)dx
a
質問されていた「本来f(x)を積分するとはf(x)にdxを掛けるという意味
なのでしょうか?」というのは、上のことより分かると思います。
dP
── は価格の成長率を表現しています。100円について2円増えた
P
としたら、これは1円当たりの成長率0.02(2%)を表しています。
これを積分すると、
dP 1
∫──=∫─dP=log|P|+C (この対数が何であるかは、私
P P
には分かりません。)