武田先生、失礼します。曲線のグラフの形状を調べる増減表について教
えていただけますでしょうか?
一般的にいって、関数の曲線の形状を調べるときに、
2次関数なら、f'(x)の1つだけについて調べて、
3次関数なら、f'(x)とf''(x)の2つについて調べて、
4次関数なら、f'(x)とf''(x)とf'''(x)の3つについて調べること
になるのですか?
それとも2次でも3次でも4次でも、一階微分と二階微分の符号を調べれ
ばいいのですか?
2次関数、3次関数、4次関数、さらに5次関数も、変数xが変数yに
変化することに変わりがないので、すべてy=f(x)と書くことが出
来る。
そのグラフは、そのxとyにより、点(x,y)ができ、それが連続的
に変化してグラフを描く。
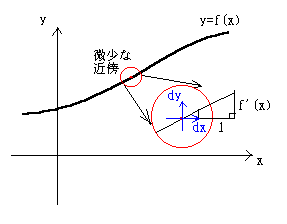
さて、微分だが、グラフ上の任意の点の微少な近傍をとれば、そこに
1次近似の直線ができる。この直線は、傾きをf′(x)とすると、
dy=f′(x)dxと表現できる。
これは第1次導関数をさす。
dy
──=f′(x)
dx
したがって、「すべての曲線は任意の点の微少な近傍で直線化する」
ことが出来ると言える。この直線の傾きから、グラフ全体の増減を推
し量ることが出来る。つまり、第1次導関数(1階微分)はすべての
曲線において増減を知る重要な役割を担っているのである。
ちょうど運動における速度の役割と同じである。
それでは第2次導関数(2階微分)はどういう働きがあるかというと、
f″(x)>0のとき、傾きf′(x)が増加していくから、グラフ
としては下に凸となる。f″(x)<0は上に凸となる。グラフの曲
がり具合を知るための働きを持っている。ちょうど運動における加速
度と同じである。
したがって、第3次導関数以降は、グラフ上も運動上も私の知る限り
では仕事がありません。
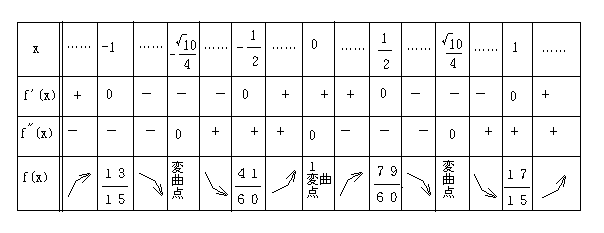
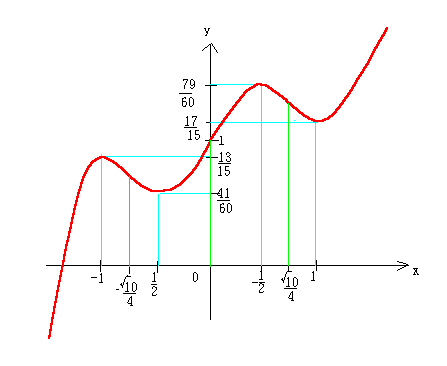
最後に、5次関数のグラフ書きを掲載します。
4 5
y=─x5 -─x3 +x+1
5 3