複素数も三角錐の体積も、全く分かりません。
誰かヒントをください。
ＳＯＳ！！

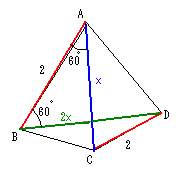
（※川口さんの解答に図や解説をつけました。武田）
武田先生こんにちは。

ayumiさんの質問で未解決の問題ですが
添削問題をやっていて同じような問題を見かけました。
一応僕の送る答案の解答を書いておきますので参考にしていただけたら
幸いです

【複素数】
αβ=(x+yi)(z+ui)=(xz-uy)+(xu+yz)i
題意より
xz-uy=x　　　　 ………… ①
8≦xu+yz≦2000　………… ②
①より　(z-1)x=uy
右辺のuyが素数の積だから、左辺も素数の積で、
z-1が素数となるのは、ｚ=3に限られる。
Ⅰ) z-1=u　、すなわち　x=y、ｚ＝3、u=2のとき
　　α=x(1+i) , β=3+2i
　　xu+yz=2x+3x=5x となり、素数とはならない。
Ⅱ) z-1=y すなわち z=3, y=2 ,x=u のとき
　　α=x+2i , β=3+xi
　　xu+yz=x² +6 　　　　　　　　　 }範囲は？
　　∴11≦x² +6≦1999　　　　　　　}8≦x² +6≦2000
　　　 5≦x² ≦1993　　　　　　　　}2≦x² ≦1994
　　　 3≦x≦43　(xは素数だから） }\(\sqrt{\quad}\)2≦x≦\(\sqrt{\quad}\)1994
　　　　　　　　　　　　　　　　　}１＜ｘ＜４５
　　　　　　　　　　　　　　　　　}ｘは素数だから（ｘ＝２も含めて）
　　この間のxの素数　x=3,5,7,11,13,17,19,23,29,31,37,41,43 に対して
　　x² +6が素数となるのは(計算が面倒です）
　　　x=5　(x² +6=31)
　　　x=11(x² +6=127)
　　　x=19(x² +6=367)
　　　x=31(x² +6=967)
　　の4個で、
　　(α,β)=(5+2i,3+5i),(11+2i,3+11i),(19+2i,3+19i),(31+2i,3+31i)

【体積】

△ABDにおいて、AからBDに下ろした垂線の足をF、△BCDにおいて、Fか
らBDに立てた垂線がBCと交わる点をEとする。
∠CBD=α,∠ABC=βとする。

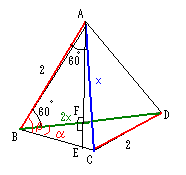
余弦定理を使って、各線分や角の大きさを計算すると、次のようになる。
BC² ＝２² ＋ｘ² －２・２・ｘcos60より、
BC=\(\sqrt{\quad}\)(x² -2x+4)
AF=2sin60=\(\sqrt{\quad}\)3,BF=2cos60=1,EF=tanα,BE=\(\frac{1}{c}\)osα
　　　　４ｘ² ＋（ｘ² －２ｘ＋４）－４
cosα＝───────────────
　　　　２・２ｘ・\(\sqrt{\quad}\)（ｘ² －２ｘ＋４）

　　　　　　　５ｘ² －２ｘ
　　　＝──────────────
　　　　４ｘ・\(\sqrt{\quad}\)（ｘ² －２ｘ＋４）

　　　　　　　５ｘ－２
　　　＝─────────────
　　　　４・\(\sqrt{\quad}\)（ｘ² －２ｘ＋４）

sin² α＝１－cos² αより、
　　　　　\(\sqrt{\quad}\)(60-12x-9x² )
sinα=───────────
　　　　　４\(\sqrt{\quad}\)(x² -2x+4)

　　　　（ｘ² －２ｘ＋４）＋４－ｘ²
cosβ＝───────────────
　　　　　２・２・\(\sqrt{\quad}\)(x² -2x+4)

　　　　　　　－２ｘ＋８
　　　＝──────────
　　　　　４・\(\sqrt{\quad}\)(x² -2x+4)

　　　　　　　－ｘ＋４
　　　＝──────────
　　　　　２・\(\sqrt{\quad}\)(x² -2x+4)}sin² β＝１－cos² βより、
　　　　　　　\(\sqrt{\quad}\)３ｘ
sinβ=───────────
　　　　　２・\(\sqrt{\quad}\)(x² -2x+4)

　　　　　　１　　　　　　　　１
AE² ＝４＋────－２・２・───・cosβ
　　　　　cos² α　　　　　　cosα

∠AFE=θとすると、
　　　　AF² ＋FE² －AE²
cosθ＝─────────
　　　　２・AF・FE

　　　　（\(\sqrt{\quad}\)３）² ＋tan² α－AE²
　　　＝─────────────
　　　　　　　２・\(\sqrt{\quad}\)３・tanα

　　　　　　　　　　　4cos² α+1-4cosαcosβ
　　　　　3+tan² α－────────────
　　　　　　　　　　　　　　cos² α
　　　＝───────────────────
　　　　　　　　　　2\(\sqrt{\quad}\)3 tanα

　　　　　３cos² α＋sin² α－４cos² α－１＋４cosαcosβ
　　　＝──────────────────────────
　　　　　　　　　　　２\(\sqrt{\quad}\)３sinαcosα

　　　　sin² α－cos² α－（sin² α＋cos² α）＋４cosαcosβ
　　　＝──────────────────────────
　　　　　　　　　　　２\(\sqrt{\quad}\)３sinαcosα

　　　　　－２cos² α＋４cosαcosβ
　　　＝─────────────────
　　　　　　　２\(\sqrt{\quad}\)３sinαcosα

　　　　　２cosβ－cosα
　　　＝─────────
　　　　　　\(\sqrt{\quad}\)３sinα
sin² θ＝１－cos² θより、
　　　　　　　（２cosβ－cosα）²
sin² θ＝１－────────────
　　　　　　　　　３sin² α
この式に上で求めた各値を代入して、sin² θを計算すると、
　　　　　-12x² +32x-16
sin² θ＝────────
　　　　　20-4x-3x²
したがって、
　　　　\(\sqrt{\quad}\)（-12x² +32x-16）
sinθ＝────────────
　　　　　\(\sqrt{\quad}\)（20-4x-3x² ）

Aから下ろした三角錐の高さをhとすると
　　　　　　　　　\(\sqrt{\quad}\)｛３・（-12x² +32x-16）｝
ｈ＝\(\sqrt{\quad}\)３・sinθ＝───────────────
　　　　　　　　　　　\(\sqrt{\quad}\)（20-4x-3x² ）

△BCDの面積Sは　　　１　　　　　　　１
　Ｓ＝─・BD・BCsinα=─・ｘ・\(\sqrt{\quad}\)｛３・(20-4x-3x² )｝
　　　２　　　　　　　４
体積は、三角錐だから底面積×高さ÷３より、
　　１　ｘ　\(\sqrt{\quad}\)｛3(20-4x-3x² )｝　\(\sqrt{\quad}\)｛3(-12x² +32x-16)｝
Ｖ＝─・─・──────────・───────────
　　３　４　　　　　　１　　　　　\(\sqrt{\quad}\)(-20-4x-3x² )

　　ｘ
　＝─・\(\sqrt{\quad}\)｛４(-3x² +8x-4)｝
　　４

　　ｘ
　＝─・\(\sqrt{\quad}\)(-3x² +8x-4)
　　２

-3x² +8x-4>0より、解は、\(\frac{2}{3}\)＜x＜2 の範囲となる。
ｘを\(\sqrt{\quad}\)の中に入れて、\(\sqrt{\quad}\)の中の4次式をf(x)とおいて、
f(x)=-3x⁴ +8x³ -4x²
を微分して、
f′(x)＝-12x³ +24x² -8x
　　　＝-4x(3x² -6x+2)
f′(x)=0　より、ｘ＝０，３ｘ² －６ｘ＋２＝０
解の公式より、
　　３\(\pm\)\(\sqrt{\quad}\)（９－６）　３\(\pm\)\(\sqrt{\quad}\)３
ｘ＝────────＝────
　　　　　３　　　　　　　３
\(\frac{2}{3}\)＜x＜2 の範囲内で増減表を作り、体積が最大となるxを求めると

ｘ　　｜\(\frac{2}{3}\) ｜………｜(3+\(\sqrt{\quad}\)3)/3 ｜………｜２　｜
────────────────────────
f′(x)｜　　｜　＋　｜　　０　　｜　－　｜　　｜
────────────────────────
f(x)　｜　　｜増　加｜　最　大　｜減　少｜　　｜

　　　３＋\(\sqrt{\quad}\)３
∴ｘ＝────　……（答）
　　　　　３