質問＜３４８＞２０００／１０／２９－３０
from=あつ
「二次関数」

二次関数ｙ=Ｘ＾２＋ａＸ＋ｂがＹ＝－２Ｘ＋２と
０≦Ｘ≦２の間でだだ一つ交わる時の
（ａ、ｂ）の範囲を求めよ。
（接するときも含む）←訂正がありました！

解答を見たのですが
場合分けが多すぎてよくわかりません。
よろしくお願いします。

お返事２０００／１０／２９－３０
from=武田

連立
｛ｙ＝ｘ2 ＋ａｘ＋ｂ
｛ｙ＝－２ｘ＋２
が交わるか接するかどうかは、
ｘ2 ＋ａｘ＋ｂ＝－２ｘ＋２
ｘ2 ＋（ａ＋２）ｘ＋（ｂ－２）＝０
の方程式の解が１つ、２つあるかどうかである。
そのことは、
ｆ（ｘ）＝ｘ2 ＋（ａ＋２）ｘ＋（ｂ－２）のグラフが
ｘ軸と交わるか、ｘ軸と接するかだから、
ｘの範囲０≦ｘ≦２で、１つだけ交わるかまたは、接する
ものを探せばよい。
次のような場合分けの中で、②③④と⑥⑦⑨⑩の場合が問に該当する。

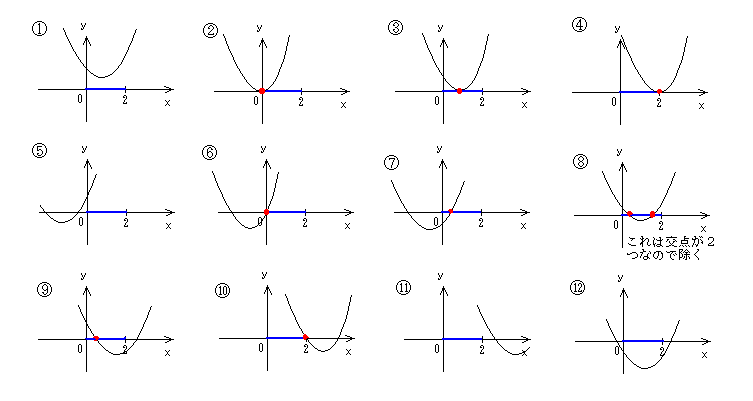
②③④の場合
判別式Ｄ＝（ａ＋２）2 －４（ｂ－２）＝０より、
　　１
ｂ＝─（ａ＋２）2 ＋２　……（Ａ）
　　４
ｆ（０）＝ｂ－２＝０より、ｂ＝２
　　１
２＝─（ａ＋２）2 ＋２　∴ａ＝－２　∴（－２，２）
　　４
ｆ（２）＝４＋２（ａ＋２）＋（ｂ－２）＝０より、ｂ＝－２ａ－６
　　　　　　１
－２ａ－６＝─（ａ＋２）2 ＋２
　　　　　　４
－８ａ－２４＝ａ2 ＋４ａ＋４＋８
ａ2 ＋１２ａ＋３６＝０
（ａ＋６）2 ＝０
∴ａ＝－６　∴ｂ＝－２（－６）－６＝６　∴（－６，６）
０≦ｘ≦２より、グラフ（Ａ）の上で、（－６，６）から（－２，２）
までは答えの範囲である。

⑥⑦の場合
判別式Ｄ＝（ａ＋２）2 －４（ｂ－２）＞０より、
　　１
ｂ＜─（ａ＋２）2 ＋２
　　４
ｆ（０）＝ｂ－２≦０より、ｂ≦２
ｆ（２）＝４＋２（ａ＋２）＋（ｂ－２）＞０より、
ｂ＞－２ａ－６

⑨⑩の場合
判別式Ｄ＝（ａ＋２）2 －４（ｂ－２）＞０より、
　　１
ｂ＜─（ａ＋２）2 ＋２
　　４
ｆ（０）＝ｂ－２＞０より、ｂ＞２
ｆ（２）＝４＋２（ａ＋２）＋（ｂ－２）≦０より、
ｂ≦－２ａ－６

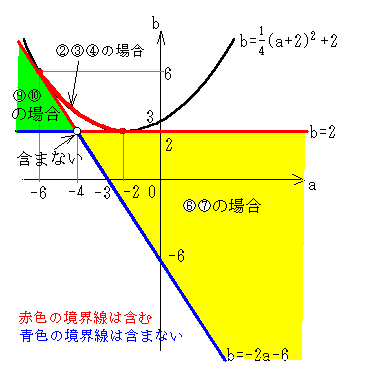
以上の３つの場合をまとめたものが、以下の範囲となる。
これが、（ａ，ｂ）の範囲である。