問１

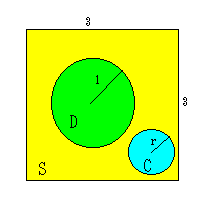
一辺３の正方形Ｓの中に円板ＣとＤを動かして、Ｃは半径ｒを０＜ｒ＜１／２
の間を伸び縮させて動き回ると、いろいろな部分に面積をとることが出来る。
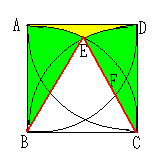
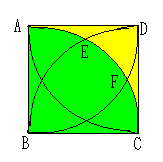
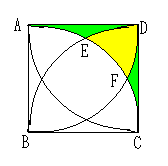
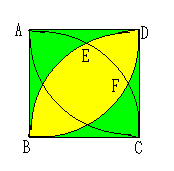
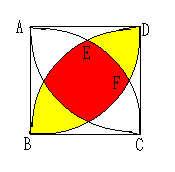
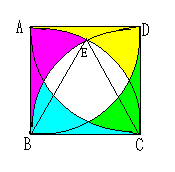
しかし、半径１の円板Ｄの４隅に取った円の共通部分はどのようにＤが動き回
っても円板Ｄの中にあるので、

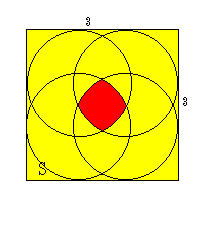
円板Ｃが動き回れる面積は、この赤色の部分以外の面積となる。
赤色の部分の面積を求めると、
π
─＋１－\(\sqrt{\quad}\)３
３
　↑下にお便りを頂いた岡崎さんから符号の誤りを指摘されましたので、
　　もう一度、積分してみたところ、誤っていましたので、訂正しました。
　　感謝！！

したがって、
　　　　　π　　　　　　　　　　　　π
Ｓ＝９－（─＋１－\(\sqrt{\quad}\)３）＝８＋\(\sqrt{\quad}\)３－─　……（答）
　　　　　３　　　　　　　　　　　　３

　≒８＋１．７３２－１．０４７＝８．６８５
　　　　　　　　　　　　　　　　小数化すると

問２

─→　─→
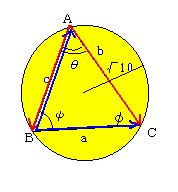
ＡＢ・ＡＣ＝８より、ｂｃcosθ＝８
ａ² ＝ｂ² ＋ｃ² －２ｂｃcosθ
　　＝ｂ² ＋ｃ² －２×８
　　＝ｂ² ＋ｃ² －１６……①

─→　─→
ＢＡ・ＢＣ＝１２より、ａｃcosψ＝１２
ｂ² ＝ａ² ＋ｃ² －２ａｃcosψ
　　＝ａ² ＋ｃ² －２×１２
　　＝ａ² ＋ｃ² －２４……②

①＋②より、
ａ² ＋ｂ² ＝ｂ² ＋ａ² ＋２ｃ² －４０
２ｃ² ＝４０
ｃ² ＝２０
ｃ＞０より、
∴ｃ＝２\(\sqrt{\quad}\)５……（答）

※またまた、岡崎さんからアドバイスを頂きました。２番目のお便りを
ご覧下さい。感謝！！

問１
「質問３９７問１の下の図の赤い部分の面積
　　　　　　　　　　　を求める初等幾何的方法」

質問３９７問１は、「武田さんからのお返事」の中の下の図において、
右上の円と左下の円の交点のうち左上の点をＡ、右下の点をＣとします。
左上と右下の円の交点のうち左下の点をＢ、右上の点をＤとすると
点Ａ、Ｂ、Ｃ、Ｄは各円の中心であり、四角形ＡＢＣＤは正方形です。
さらに、左下の円と右下の円の交点のうち上の点をＥ
左上と左下の円の交点のうち、右側の点をＦとします。

以下は、この正方形ＡＢＣＤの中だけで考えて
「武田さんからのお返事」の下の図の赤い部分の面積を求めます。


三角形ＢＣＥは正三角形です。
また、点Ｂは左下の円の中心ですので、線分ＡＢ、線分ＢＥ、
左下の円の一部ＡＥで囲まれた部分は、中心角３０度の扇形です。
同様に、線分ＣＤ、線分ＣＥ、円の一部ＥＤで囲まれた部分は扇形です。
左下の円の一部ＡＥと右下の円の一部ＥＤと線分ＡＤで囲まれた図形ＡＥＤ
（以下、図形ＡＥＤとする）の面積は、
（図形ＡＥＤ）＝（正方形ＡＢＣＤ）－（正三角形ＢＣＥ）－（扇形ＡＢＥ）
　　　　　　　　－（扇形ＥＣＤ）
　　　　　　　　　　　　１　　　　　　　　　　　　１　　　　π
　　　　　　　＝１×１－─×１² ×sin６０°－２×──×１² ×─
　　　　　　　　　　　　２　　　　　　　　　　　　２　　　　６

　　　　　　　　　　\(\sqrt{\quad}\)３　π
　　　　　　　＝１－──－─
　　　　　　　　　　　４　６
で求められます。


線分ＡＤ、線分ＣＤ、左下の円の一部ＡＣで囲まれた部分を図形ＡＣＤ、
線分ＡＢ、線分ＢＣ、左下の円の一部ＡＣで囲まれた扇形を扇形ＡＢＣと
すると、図形ＡＣＤの面積は、
（図形ＡＣＤ）＝（正方形ＡＢＣＤ）－（扇形ＡＢＣ）
　　　　　　　　　　　　１　　　　π
　　　　　　　＝１×１－─×１² ×─
　　　　　　　　　　　　２　　　　２

　　　　　　　　　　π
　　　　　　　＝１－─
　　　　　　　　　　４
で求められます。


右下の円の一部ＤＥ、左下の円の一部ＥＦ、左上の一部ＤＦで囲まれた
部分を図形ＤＥＦとすると、この面積は、
（図形ＤＥＦ）＝（図形ＡＣＤ）－２×（図形ＡＥＤ）
　　　　　　　　　　　π　　　　　　　\(\sqrt{\quad}\)３　π
　　　　　　　＝（１－─　）－２（１－──－─　）
　　　　　　　　　　　４　　　　　　　　４　６

　　　　　　　　　π　　　\(\sqrt{\quad}\)３
　　　　　　　＝──－１＋──
　　　　　　　　１２　　　　２
で求められます。


左上の円の一部ＢＤと右下の円の一部ＢＤで囲まれた部分を図形ＢＤ
線分ＡＢ、線分ＡＤ、左上の円の一部ＢＤで囲まれた扇形を扇形ＡＢＤ
線分ＢＣ、線分ＣＤ、右下の円の一部ＢＤで囲まれた扇形を扇形ＢＣＤ
とすると、図形ＢＤの面積は、
（図形ＢＤ）＝（扇形ＡＢＤ）＋（扇形ＢＣＤ）－（正方形ＡＢＣＤ）
　　　　　　　１　　　　π　１　　　　π
　　　　　　＝─×１² ×─＋─×１² ×─－１×１
　　　　　　　２　　　　２　２　　　　２

　　　　　　　π
　　　　　　＝─－１
　　　　　　　２
で求められます。


赤い部分の面積は、
（赤い部分の面積）＝（図形ＢＤ）－２×（図形ＤＥＦ）
　　　　　　　　　　　π　　　　　　　π　　　\(\sqrt{\quad}\)３
　　　　　　　　　＝（─－１）－２（──－１＋──　）
　　　　　　　　　　　２　　　　　　１２　　　　２

　　　　　　　　　　π
　　　　　　　　　＝─＋１－\(\sqrt{\quad}\)３　……（答）
　　　　　　　　　　３
で求めることができます。

問２
質問３９７問１へのコメントを早速きれいな図をいれて
ホームルームに載せていただきありがとうございました。
図はどのようなソフトで描いているのですか。

乗りかかった船ですので、質問３９７問２についても考えてみました。

少し古い高校の参考書（昭和５５年発行）を見ていたら、
余弦定理のところに、第一余弦定理と第二余弦定理の２つが書いてあり
ました。
第二余弦定理は現在の教科書にも載っている、
a＾２＝ｂ＾２＋ｃ＾２－２ｂｃ・ｃｏｓＡ
ｂ＾２＝ｃ＾２＋a＾２－２ｃａ・ｃｏｓＢ
ｃ＾２＝a＾２＋ｂ＾２－２ａｂ・ｃｏｓＣ
です。
第一余弦定理は、
ａ＝ｂ・ｃｏｓＣ＋ｃ・ｃｏｓＢ
ｂ＝ｃ・ｃｏｓＡ＋ａ・ｃｏｓＣ
ｃ＝ａ・ｃｏｓＢ＋ｂ・ｃｏｓＡ
です。
この第一余弦定理を使うと、
質問３９７問２の辺ＡＣ、ＢＣの長さを求めることができると思うのですが。

以下記号は武田さんのホームページの記号を使います。

質問３９７問２（１）の解より、ｃ＝２\(\sqrt{\quad}\)５　であり、
外接円の半径が\(\sqrt{\quad}\)１０ですので、
正弦定理から、φ＝４５°または１３５°です。

条件の内積の式から得られる、ｃｂ・ｃｏｓθ＝８と、
ｃａ・ｃｏｓψ＝１２にｃの値を代入した式を、
２\(\sqrt{\quad}\)５・ｃｏｓθ＝８／ｂ、２\(\sqrt{\quad}\)５・ｃｏｓψ＝１２／ａ　と変形して、
ｃとφの値を第一余弦定理のａ＝の式とｂ＝の式に代入した式にあてはめると、
ａとｂの式が２つできます。
｛ａ＝ｂ・ｃｏｓφ＋２\(\sqrt{\quad}\)５・ｃｏｓψ＝ｂ・ｃｏｓφ＋１２／ａ……①
｛ｂ＝２\(\sqrt{\quad}\)５・ｃｏｓθ＋ａ・ｃｏｓφ＝８／ｂ＋ａ・ｃｏｓφ　……②

この連立方程式を解くことによって
ａとｂを求めることができると思います。
①×ａ－②×ｂ
　　ａ² ＝ａｂ・ｃｏｓφ＋１２
－）ｂ² ＝８＋ａｂ・ｃｏｓφ
───────────────
　　ａ² －ｂ² ＝４

　　ｂ＝\(\pm\)\(\sqrt{\quad}\)（ａ² －４）


（※再度アドバイスがありましたので、以下訂正します。感謝！！）

ｂ＞０より、ｂ＝\(\sqrt{\quad}\)（ａ² －４）……③
①に、φ＝４５°または１３５°より、
φ＝４５°のときはｃｏｓφ＝１／\(\sqrt{\quad}\)２ですが、
φ＝１３５°のときはｃｏｓφ＝－１／\(\sqrt{\quad}\)２ですので
以下の２行は場合分けが必要だが、\(\pm\)とまとめて計算すると、
　　　　\(\pm\)１　１２
ａ＝ｂ・──＋──
　　　　\(\sqrt{\quad}\)２　　ａ
\(\sqrt{\quad}\)２ａ² ＝\(\pm\)ａｂ＋１２\(\sqrt{\quad}\)２

③を代入して、
\(\sqrt{\quad}\)２ａ² ＝\(\pm\)ａ・｛\(\sqrt{\quad}\)（ａ² －４）｝＋１２\(\sqrt{\quad}\)２
\(\pm\)ａ・｛\(\sqrt{\quad}\)（ａ² －４）｝＝\(\sqrt{\quad}\)２ａ² －１２\(\sqrt{\quad}\)２
両辺を２乗して、
ａ² ・（ａ² －４）＝２ａ⁴ －４８ａ² ＋２８８
ａ⁴ －４ａ² ＝２ａ⁴ －４８ａ² ＋２８８
ａ⁴ －４４ａ² ＋２８８＝０
（ａ² －３６）（ａ² －８）＝０
ａ² ＝３６またはａ² ＝８
ａ＝\(\pm\)６または\(\pm\)２\(\sqrt{\quad}\)２
ａ＞０より、ａ＝６または２\(\sqrt{\quad}\)２……④

④を③に代入して、
ａ＝６のとき、ｂ＝\(\sqrt{\quad}\)（３６－４）＝\(\sqrt{\quad}\)３２＝４\(\sqrt{\quad}\)２
ａ＝２\(\sqrt{\quad}\)２のとき、ｂ＝\(\sqrt{\quad}\)（８－４）＝\(\sqrt{\quad}\)４＝２
｛ａ＝６、ｂ＝４\(\sqrt{\quad}\)２
｛ａ＝２\(\sqrt{\quad}\)２、ｂ＝２

（答）｛ａ＝６、ｂ＝４\(\sqrt{\quad}\)２、ｃ＝２\(\sqrt{\quad}\)５のときは、φ＝４５°の三角形
　　　｛ａ＝２\(\sqrt{\quad}\)２、ｂ＝２、ｃ＝２\(\sqrt{\quad}\)５のときは、φ＝１３５°の三角形

４枚の楓（かえで）の面積をまず求める。黄色、緑、水色、ピンクの４枚
である。
△ＥＢＣが正三角形だから、∠ＥＣＢ＝６０°、∠ＡＢＥ＝３０°
扇形ＡＢＥの面積＝π×１²×（３０°／３６０°）
　　　　　　　　　　π
　　　　　　　　＝――
　　　　　　　　　１２
扇形ＥＢＣの面積＝π×１²×（６０°／３６０°）
　　　　　　　　　π
　　　　　　　　＝―
　　　　　　　　　６
　　　　　　　　　　　１　　　　　　　　　　　\(\sqrt{\quad}\)３
正三角形ＥＢＣの面積＝―×１×sin６０°×１＝―――
　　　　　　　　　　　２　　　　　　　　　　　　４

楓ＡＢＥの面積＝扇形ＡＢＥの面積－（扇形ＥＢＣの面積－正三角形ＥＢＣの面積）
　　　　　　　　　π　　π　\(\sqrt{\quad}\)３　　π－２π＋３\(\sqrt{\quad}\)３
　　　　　　　＝――－（―－――）＝――――――――
　　　　　　　　１２　　６　　４　　　　　１２

　　　　　　　　３\(\sqrt{\quad}\)３－π
　　　　　　　＝―――――
　　　　　　　　　　１２
　　　　　　　　　　　　　　　　　　　　３\(\sqrt{\quad}\)３－π　　　　　　π
目的の解答の白い部分の面積＝１×１－４×―――――＝１－\(\sqrt{\quad}\)３＋―………（答）
　　　　　　　　　　　　　　　　　　　　　　１２　　　　　　　３