2次不等式の基本的な事から全くわかりません。教えて下さい。
不等式を、関数のグラフと関連づけながら説明しましょう。
併せて式変形の方も付記します。
①一次関数と一次不等式の場合
「一次不等式2x+4>0を解け。」
<関数のグラフとの関連>
2x+4>0は、一次関数y=2x+4のグラフの
y>0にあたる。
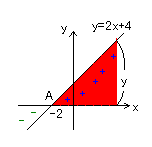
図より、+の部分は、x>-2のとき
したがって、(答)x>-2
<式変形>
2x+4>0
両辺に(-4)を加えると、
2x+4+(-4)>0+(-4)
2x>-4……移項したと見る。
両辺を2で割ると、
(2x)/2>(-4)/2
(答)x>-2……xの係数の2で割ると見る。
②二次関数と二次不等式の場合
「二次不等式x2+2x-3>0を解け。」
<関数のグラフとの関連>
二次方程式x2+2x-3=0を解く。
x=-3,1
x2+2x-3>0は、
二次関数y=x2+2x-3のグラフの
y>0にあたる。
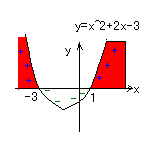
図より、+の部分は、x<-3または1<xのとき
したがって、(答)x<-3または1<x
<式変形>
x2+2x-3>0を因数分解して、
(x+3)(x-1)>0
(i) x+3>0かつx-1>0のとき
x>-3かつx>1
したがって、x>1
(ii)x+3<0かつx-1<0のとき
x<-3かつx<1
したがって、x<-3
(i)(ii)より、(答)x<-3またはx>1
「二次不等式x2+2x+3>0を解け。」
<関数のグラフとの関連>
二次方程式x2+2x+3=0を解く。
判別式D=4-12=-8<0より、
解なし
x2+2x+3>0は、
二次関数y=x2+2x+3のグラフの
y>0にあたる。
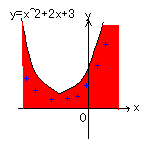
図より、+の部分は、xのすべての数のとき
したがって、(答)xはすべての数
<式変形>
x2+2x+3>0を平方完成して、
(x+1)2+2>0
(x+1)2≧0
(答)xはすべての数
「二次不等式x2+2x+1≦0を解け。」
<関数のグラフとの関連>
二次方程式x2+2x+1=0を解く。
(x+1)2=0
x=-1(重解)
x2+2x+1≦0は、
二次関数y=x2+2x+1のグラフの
y≦0にあたる。
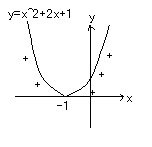
図より、-の部分または0の部分は、x=-1のみ
したがって、(答)x=-1
<式変形>
x2+2x+1≦0を因数分解して、
(x+1)2≦0
(x+1)2<0は、解なし
(x+1)2=0は、x=-1
(答)x=-1